개요
일반적으로, 우리는 자바 HashMap이 평균적으로 O(1)의 시간 복잡도를 가진다고 배웁니다.
하지만 “해시 충돌(Hash Collision)”이 심해지면 성능이 급격히 떨어질 수 있다는 사실은 자칫 놓치기 쉽습니다. 또한, CPU 캐시 구조와 “참조 지역성(Reference Locality)”을 이해하면, 왜 이 문제가 현실에서 더 크게 체감되는지 알 수 있습니다.
이 주제는 백준 7453 번 문제를 풀다가 경험하게 되었는데
https://www.acmicpc.net/problem/7453
C++,C 에서는 기존의 방법처럼 2개씩 쌍으로 묶어서 계산한다음에 한쪽 값을 해시 맵에 넣어두고 0을 만들기 위한 보수가 존재하는지 hash key 탐색으로 풀렸지만 자바의 경우에는 그렇지 않았다.
탐색 길이인 n은 4000*4000 으로 16,000,000 정도로 1.6천만 정도 되는데 이론상 O(1) 이기에 스무스 하게 통과를 해야만 한다.
포스팅에서 배우겠지만 해시 저격으로 인해 버킷 적중이 8회(기본값)이 넘어가 Red-Black Tree 로 변환되고 이는 O(logN)으로 동작하지만, 그래도 충분히 느리기 때문에 해당 방법으로 끝까지 풀리지 않았다.
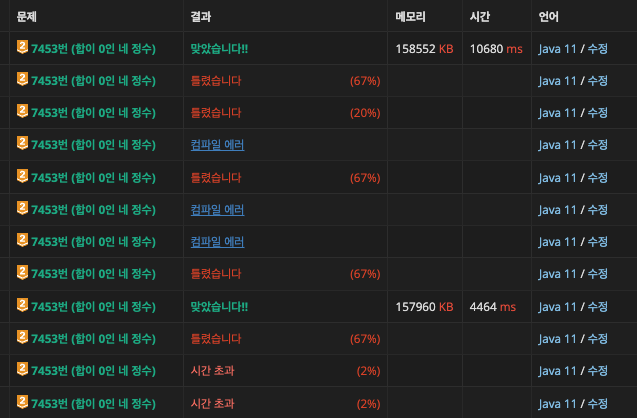
결국 이분탐색이나 투포인터로 문제를 해결했어야했다.
따라서
이 글에서는
- 참조 지역성이란 무엇인지
- 왜 자바 HashMap에 해시 충돌이 발생하면 성능이 크게 떨어지는지
- 직접 해볼 수 있는 ‘악의적 입력(Adversarial Input)’ 예시
1. 참조 지역성(Reference Locality)이란?
1.1 정의
참조 지역성이란 컴퓨터 프로그램이 메모리를 접근할 때, 일정 시점에 가까운 주소나 최근에 사용한 주소를 다시 참조하는 경향이 있다는 개념입니다.CPU는 이 패턴을 이용해 캐시(Cache)라는 작은 저장장치에 데이터를 미리 가져오고, 필요한 데이터를 재활용하여 빠른 접근 속도를 가능하게 합니다.
1.2 두 가지 주요 형태
- 시간적 지역성(Temporal Locality): 한 번 참조된 데이터는 가까운 미래에 다시 참조될 가능성이 높다.
- 공간적 지역성(Spatial Locality): 어떤 주소가 참조되면, 그 근처(인접) 주소를 곧 사용할 가능성이 높다.
1.3 컬렉션 자료구조와 지역성
- 배열(Array): 내부가 연속된 메모리로 이뤄져 있으므로, 순차 탐색 시 공간적 지역성이 극대화된다.
- 연결 리스트(LinkedList): 노드가 임의 메모리 주소에 산재해 있으므로, 노드를 차례대로 탐색할 때 CPU 캐시에 잘 실리지 않는다.
- 해시 테이블(HashMap): 해시 버킷(배열)은 연속적일 수 있지만, 충돌이 발생하면 연결 리스트나 트리를 따라가야 한다. 이 과정에서 임의 주소를 점프하므로 지역성이 떨어질 수 있다.
2. 자바 HashMap, 정말 O(1)일까?
2.1 평균 O(1)의 비밀
자바 HashMap은 평균적으로 put, get, containsKey 연산 모두 O(1)에 가깝습니다.
https://medium.com/geekculture/a-deep-dive-into-java-8-hashmap-a976aca22f9b
A Deep Dive into Java 8 HashMap
The main data structures in HashMap include Array, LinkedList, and Red-Black Tree (an advanced version of a binary search tree). This…
medium.com
2.2 최악 O(N) 시나리오
그러나 해시 충돌이 심각해지면, 특정 버킷에 매우 많은 원소가 쌓여버릴 수 있습니다.
자바 8 이상에서 충돌 처리 방식
자바 8부터는 체이닝을 단순히 연결 리스트로 처리하는 방식에서 개선됨:
- 초기에는 LinkedList를 사용
- 충돌이 많이 발생하여 같은 버킷에 8개 이상의 엔트리가 들어가면, Red-Black Tree로 변환
- 이로 인해 해시 충돌이 많아도 탐색 성능이 O(log n) 으로 향상됨 (기존 O(n) → 개선 O(log n))
위처럼, 이를 해결 하기위해서 자바 8 부터는 특정 횟수 이상으로 충돌이 일어나면 logN인 트리맵 구조로 찾아내지만 이 또한 특정 상황에서는 부족한 경우가 있다.
아까의 백준 문제를 예시로 들자면,
해시 사용
- ab[] 생성: O(N^2)
- cd[] 돌면서 N^2개 해시 키 서칭: O(1*N^2)
- 삽입, 조회시에 O(1)이지만 충돌이 심하면 달라질수 있음.logN ~ 그이상.
- 충돌시에 트리화 비용까지 생각한다면 최악 O(N^3~N^2 log(N^2))
이진 탐색이나 투포인터가 시간 복잡도는 크지만 충돌로 인한 딜레이를 고려한다면 더 효율적인 선택이 되는것이다.
이진 탐색
- ab[], cd[] 생성: 각각 O(N^2)
- 정렬: O(N^2 log(N^2)) = O(N^2 log N)
- ab[] 순회(=N^2) × 이분 탐색(log(N^2)) → O(N^2 log N)
- 전체적으로 O(N^2 log N)
투포인터
- ab[], cd[] 생성: O(N^2)
- 정렬: O(N^2 log(N^2)) = O(N^2 log N)
- 투 포인터: O(N^2) (중간에 i++, j-- 형태로 한쪽만 움직이므로 한 바퀴 돌면 종료)
- 전체적으로 O(N^2 log N)
2.3 지역성과의 결합 효과
해시 충돌이 많이 날수록, 버킷을 찾아갔을 때 임의 주소를 다수 탐색해야 합니다.
3. 직접 해보는 해시 충돌 극단 사례, HashMap/ArrayList 참조지역성 테스트
1. 반 강제적인 해시 충돌 시행
import java.util.HashMap;
import java.util.Map;
public class ExtremeHashCollision {
// 해시 코드가 항상 같은 '악의적'인 키
static class BadKey {
private final int value;
public BadKey(int value) {
this.value = value;
}
@Override
public int hashCode() {
return 42; // 모든 객체가 동일한 해시 코드
}
@Override
public boolean equals(Object o) {
// value만 같으면 equals true
if (this == o) return true;
if (!(o instanceof BadKey)) return false;
BadKey other = (BadKey) o;
return this.value == other.value;
}
}
public static void main(String[] args) {
// N이 클수록 충돌이 극단적으로 많아짐
int N = 500_000; // 50만, 100만 등으로 늘리면 심각하게 느려질 수 있음
Map<BadKey, Integer> map = new HashMap<>(N);
long start = System.nanoTime();
// (1) put 연산
for (int i = 0; i < N; i++) {
map.put(new BadKey(i),i);
}
long afterPut = System.nanoTime();
// (2) get 연산 (전부 있는 키)
long sum = 0;
for (int i = 0; i < N; i++) {
sum += map.get(new BadKey(i));
}
long afterGet = System.nanoTime();
System.out.printf("Insertion took: %.3f ms\n", (afterPut - start) / 1e6);
System.out.printf("Lookup took: %.3f ms\n", (afterGet - afterPut) / 1e6);
System.out.println("Sum check = " + sum);
}
}
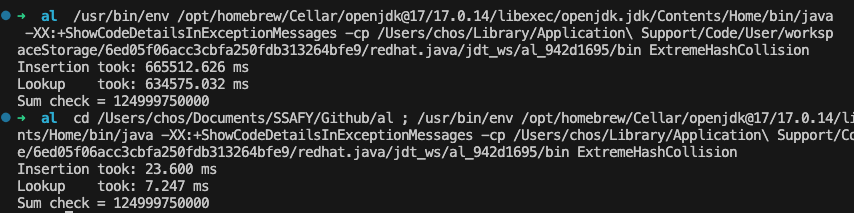
극단 적인 값(50만개, 전부 같은 해시키) 를 넣긴 했지만 충돌시 많은 비용이 드는걸 알수 있다.
2. HashMap 과 ArrayList 참조 지역성 (접근시간) 테스트
import java.util.*;
public class LocalityTest {
public static void main(String[] args) {
final int[] SIZES = {10_000, 100_000, 1_000_000, 10_000_000};
for (int SIZE : SIZES) {
System.out.println("Testing with SIZE: " + SIZE);
// HashMap 준비
Map<Integer, Integer> hashMap = new HashMap<>(SIZE);
for (int i = 0; i < SIZE; i++) {
hashMap.put(i, i);
}
// TreeMap 준비
Map<Integer, Integer> treeMap = new TreeMap<>();
for (int i = 0; i < SIZE; i++) {
treeMap.put(i, i);
}
// ArrayList 준비
List<Integer> arrayList = new ArrayList<>(SIZE);
for (int i = 0; i < SIZE; i++) {
arrayList.add(i);
}
// JIT 최적화 방지 및 GC 영향 제거
int sum = 0;
System.gc();
// HashMap 접근 시간
long startHash = System.nanoTime();
for (int i = 0; i < SIZE; i++) {
sum += hashMap.get(i); // 최적화 방지
}
long endHash = System.nanoTime();
System.out.println("HashMap 조회 시간(ns): \t\t" + (endHash - startHash));
// TreeMap 접근 시간
long startTree = System.nanoTime();
for (int i = 0; i < SIZE; i++) {
sum += treeMap.get(i); // 최적화 방지
}
long endTree = System.nanoTime();
System.out.println("TreeMap 조회 시간(ns): \t\t" + (endTree - startTree) +
" (logN: " + String.format("%.2f", Math.log(SIZE) / Math.log(2)) + ")");
// ArrayList 접근 시간
long startList = System.nanoTime();
for (int i = 0; i < SIZE; i++) {
sum += arrayList.get(i); // 최적화 방지
}
long endList = System.nanoTime();
System.out.println("ArrayList 조회 시간(ns): \t" + (endList - startList));
// 결과 확인
System.out.println("검증용 sum 값: " + sum);
System.out.println();
}
}
}ArrayList 접근 시간은 gc나 JIT 컴파일러로 인한 오버헤드나 최적화 등을 고려해서 코드를 구성했다.
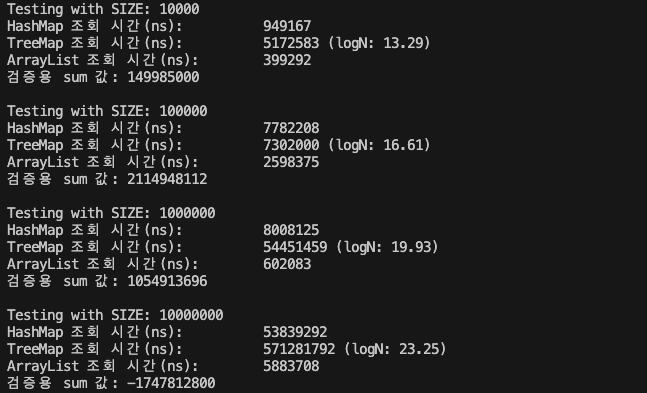
TreeMap이 HashMap 에 비해서 터무니없이 느릴수 있다 생각할수 있지만 테스트 1의 경우를 미루어 보면 최악의 HashMap(충돌)에 비해서는 평균적으로 준수한 성능을 낸다.
- ArrayList (O(1))
- 단순한 배열 인덱스 접근 → 캐시 친화적 & 빠름
- 데이터 크기 증가해도 성능 저하 거의 없음.
- HashMap (O(1) 평균, O(n) 최악)
- 일반적으로 해시 충돌이 적으면 빠름.
- 충돌이 많아질수록 성능이 저하될 가능성이 있음.
- TreeMap (O(log n))
- 내부적으로 Red-Black Tree(균형 이진 탐색 트리) 사용.
- 조회 성능이 항상 O(log n)으로 유지됨.
- 데이터 크기가 커질수록 HashMap보다 느리지만, 최악의 경우에는 HashMap보다 안정적인 성능을 유지.
그래서 언제 뭘 써야하나?
- 데이터 크기가 작을 때
- HashMap > TreeMap (둘 다 빠름)
- ArrayList는 인덱스 조회용으로 유리
- 데이터 크기가 클 때
- TreeMap은 항상 O(log n), 성능이 일정하지만 HashMap보다 느림.
- HashMap은 충돌이 많으면 TreeMap보다 더 느려질 수 있음.
- ArrayList는 조회가 많을 때 가장 빠름.
- 정렬이 필요하면?
- TreeMap은 정렬된 데이터를 유지하므로 탐색이 빈번한 경우에는 유용.
4. 해결책 또는 예방법
- 입력 데이터 특성 파악
- TreeMap 활용
- HashMap 최적화 파라미터 조정
- 참조 지역성 개선
이라고 제시를 해주고 있지만 코드포스나 자유게시판의 글을 확인 해보면
- 데이터가 지나치게 많거나(예: 수천만 건 이상),
- 해시 저격 패턴(Adversarial input)이 의심될 때,
- N^2 루프만으로도 충분히 시간을 먹을 때,
- 해시의 상수 오버헤드나 최악 상황이 부담스러울 때,
- 이럴 땐 정렬+이분 탐색(O(N^2 log N)), 투 포인터, 혹은 다른 자료구조(Map, TreeMap, Segment Tree 등)를 고려한다.
위의 경우에는 사용을 하지 않는걸 추천한다고 한다.
마무리
그럼 우리는 어떻게 이런 상황을 해결하거나 예방해야할까?
- 입력 데이터 특성 파악
- 키가 특정 패턴으로 몰리지 않도록, 혹은 악의적 패턴을 방어하고 싶다면 커스텀 해시 함수를 강화(더 균등하게)하거나,
- 해싱 대신 정렬 + 이분 탐색(TreeMap, Arrays.binarySearch 등) 같은 다른 알고리즘을 검토한다.
- TreeMap 활용
- 항상 O(log N) 복잡도이며, 해시 충돌 걱정을 덜 수 있다.
- 다만 평균적으로 HashMap보다는 상수 시간 비용이 크다.
- HashMap 최적화 파라미터
- 초기 용량(capacity)을 여유롭게 잡고, 적절한 부하율(load factor)을 설정하면 재해시(rehash) 횟수를 줄일 수 있다.
- 그러나 해시 충돌 입력 자체를 해결하진 못한다.
- 참조 지역성 개선
- 객체 접근이 분산되지 않도록, 자료구조 선택 시 연속적 메모리를 최대한 활용하면 캐시 효율이 올라간다(예: 배열, ArrayList).
- 해시맵이 불가피하다면, 무작정 큰 N 데이터가 들어오지 않도록 제한을 두거나, 다른 알고리즘으로 문제를 풀 수 있는지 고려한다.
'Java' 카테고리의 다른 글
| 조건문 없이 깔끔하게, 자바 비트마스킹으로 문제 해결하는 법 (사용 유형 정리) (0) | 2025.03.04 |
|---|---|
| 자바8 람다와 함수형 인터페이스 [3] : 디슈거링을 통한 메서드 변환과 MethodHandle, 바이트코드/JVM 분석 (1) | 2025.02.11 |
| 자바8 람다와 함수형 인터페이스 [2] : @FunctionalInterface 구현체 작성법(람다 표현식) (0) | 2025.02.11 |
| 자바8 람다와 함수형 인터페이스 [1] : 람다의 등장 배경 (0) | 2025.02.11 |
| JAVA 문법 QUIZ [2] (2) | 2025.02.04 |
개요
일반적으로, 우리는 자바 HashMap이 평균적으로 O(1)의 시간 복잡도를 가진다고 배웁니다.
하지만 “해시 충돌(Hash Collision)”이 심해지면 성능이 급격히 떨어질 수 있다는 사실은 자칫 놓치기 쉽습니다. 또한, CPU 캐시 구조와 “참조 지역성(Reference Locality)”을 이해하면, 왜 이 문제가 현실에서 더 크게 체감되는지 알 수 있습니다.
이 주제는 백준 7453 번 문제를 풀다가 경험하게 되었는데
https://www.acmicpc.net/problem/7453
C++,C 에서는 기존의 방법처럼 2개씩 쌍으로 묶어서 계산한다음에 한쪽 값을 해시 맵에 넣어두고 0을 만들기 위한 보수가 존재하는지 hash key 탐색으로 풀렸지만 자바의 경우에는 그렇지 않았다.
탐색 길이인 n은 4000*4000 으로 16,000,000 정도로 1.6천만 정도 되는데 이론상 O(1) 이기에 스무스 하게 통과를 해야만 한다.
포스팅에서 배우겠지만 해시 저격으로 인해 버킷 적중이 8회(기본값)이 넘어가 Red-Black Tree 로 변환되고 이는 O(logN)으로 동작하지만, 그래도 충분히 느리기 때문에 해당 방법으로 끝까지 풀리지 않았다.

결국 이분탐색이나 투포인터로 문제를 해결했어야했다.
따라서
이 글에서는
- 참조 지역성이란 무엇인지
- 왜 자바 HashMap에 해시 충돌이 발생하면 성능이 크게 떨어지는지
- 직접 해볼 수 있는 ‘악의적 입력(Adversarial Input)’ 예시
1. 참조 지역성(Reference Locality)이란?
1.1 정의
참조 지역성이란 컴퓨터 프로그램이 메모리를 접근할 때, 일정 시점에 가까운 주소나 최근에 사용한 주소를 다시 참조하는 경향이 있다는 개념입니다.CPU는 이 패턴을 이용해 캐시(Cache)라는 작은 저장장치에 데이터를 미리 가져오고, 필요한 데이터를 재활용하여 빠른 접근 속도를 가능하게 합니다.
1.2 두 가지 주요 형태
- 시간적 지역성(Temporal Locality): 한 번 참조된 데이터는 가까운 미래에 다시 참조될 가능성이 높다.
- 공간적 지역성(Spatial Locality): 어떤 주소가 참조되면, 그 근처(인접) 주소를 곧 사용할 가능성이 높다.
1.3 컬렉션 자료구조와 지역성
- 배열(Array): 내부가 연속된 메모리로 이뤄져 있으므로, 순차 탐색 시 공간적 지역성이 극대화된다.
- 연결 리스트(LinkedList): 노드가 임의 메모리 주소에 산재해 있으므로, 노드를 차례대로 탐색할 때 CPU 캐시에 잘 실리지 않는다.
- 해시 테이블(HashMap): 해시 버킷(배열)은 연속적일 수 있지만, 충돌이 발생하면 연결 리스트나 트리를 따라가야 한다. 이 과정에서 임의 주소를 점프하므로 지역성이 떨어질 수 있다.
2. 자바 HashMap, 정말 O(1)일까?
2.1 평균 O(1)의 비밀
자바 HashMap은 평균적으로 put, get, containsKey 연산 모두 O(1)에 가깝습니다.
https://medium.com/geekculture/a-deep-dive-into-java-8-hashmap-a976aca22f9b
A Deep Dive into Java 8 HashMap
The main data structures in HashMap include Array, LinkedList, and Red-Black Tree (an advanced version of a binary search tree). This…
medium.com
2.2 최악 O(N) 시나리오
그러나 해시 충돌이 심각해지면, 특정 버킷에 매우 많은 원소가 쌓여버릴 수 있습니다.
자바 8 이상에서 충돌 처리 방식
자바 8부터는 체이닝을 단순히 연결 리스트로 처리하는 방식에서 개선됨:
- 초기에는 LinkedList를 사용
- 충돌이 많이 발생하여 같은 버킷에 8개 이상의 엔트리가 들어가면, Red-Black Tree로 변환
- 이로 인해 해시 충돌이 많아도 탐색 성능이 O(log n) 으로 향상됨 (기존 O(n) → 개선 O(log n))
위처럼, 이를 해결 하기위해서 자바 8 부터는 특정 횟수 이상으로 충돌이 일어나면 logN인 트리맵 구조로 찾아내지만 이 또한 특정 상황에서는 부족한 경우가 있다.
아까의 백준 문제를 예시로 들자면,
해시 사용
- ab[] 생성: O(N^2)
- cd[] 돌면서 N^2개 해시 키 서칭: O(1*N^2)
- 삽입, 조회시에 O(1)이지만 충돌이 심하면 달라질수 있음.logN ~ 그이상.
- 충돌시에 트리화 비용까지 생각한다면 최악 O(N^3~N^2 log(N^2))
이진 탐색이나 투포인터가 시간 복잡도는 크지만 충돌로 인한 딜레이를 고려한다면 더 효율적인 선택이 되는것이다.
이진 탐색
- ab[], cd[] 생성: 각각 O(N^2)
- 정렬: O(N^2 log(N^2)) = O(N^2 log N)
- ab[] 순회(=N^2) × 이분 탐색(log(N^2)) → O(N^2 log N)
- 전체적으로 O(N^2 log N)
투포인터
- ab[], cd[] 생성: O(N^2)
- 정렬: O(N^2 log(N^2)) = O(N^2 log N)
- 투 포인터: O(N^2) (중간에 i++, j-- 형태로 한쪽만 움직이므로 한 바퀴 돌면 종료)
- 전체적으로 O(N^2 log N)
2.3 지역성과의 결합 효과
해시 충돌이 많이 날수록, 버킷을 찾아갔을 때 임의 주소를 다수 탐색해야 합니다.
3. 직접 해보는 해시 충돌 극단 사례, HashMap/ArrayList 참조지역성 테스트
1. 반 강제적인 해시 충돌 시행
import java.util.HashMap;
import java.util.Map;
public class ExtremeHashCollision {
// 해시 코드가 항상 같은 '악의적'인 키
static class BadKey {
private final int value;
public BadKey(int value) {
this.value = value;
}
@Override
public int hashCode() {
return 42; // 모든 객체가 동일한 해시 코드
}
@Override
public boolean equals(Object o) {
// value만 같으면 equals true
if (this == o) return true;
if (!(o instanceof BadKey)) return false;
BadKey other = (BadKey) o;
return this.value == other.value;
}
}
public static void main(String[] args) {
// N이 클수록 충돌이 극단적으로 많아짐
int N = 500_000; // 50만, 100만 등으로 늘리면 심각하게 느려질 수 있음
Map<BadKey, Integer> map = new HashMap<>(N);
long start = System.nanoTime();
// (1) put 연산
for (int i = 0; i < N; i++) {
map.put(new BadKey(i),i);
}
long afterPut = System.nanoTime();
// (2) get 연산 (전부 있는 키)
long sum = 0;
for (int i = 0; i < N; i++) {
sum += map.get(new BadKey(i));
}
long afterGet = System.nanoTime();
System.out.printf("Insertion took: %.3f ms\n", (afterPut - start) / 1e6);
System.out.printf("Lookup took: %.3f ms\n", (afterGet - afterPut) / 1e6);
System.out.println("Sum check = " + sum);
}
}

극단 적인 값(50만개, 전부 같은 해시키) 를 넣긴 했지만 충돌시 많은 비용이 드는걸 알수 있다.
2. HashMap 과 ArrayList 참조 지역성 (접근시간) 테스트
import java.util.*;
public class LocalityTest {
public static void main(String[] args) {
final int[] SIZES = {10_000, 100_000, 1_000_000, 10_000_000};
for (int SIZE : SIZES) {
System.out.println("Testing with SIZE: " + SIZE);
// HashMap 준비
Map<Integer, Integer> hashMap = new HashMap<>(SIZE);
for (int i = 0; i < SIZE; i++) {
hashMap.put(i, i);
}
// TreeMap 준비
Map<Integer, Integer> treeMap = new TreeMap<>();
for (int i = 0; i < SIZE; i++) {
treeMap.put(i, i);
}
// ArrayList 준비
List<Integer> arrayList = new ArrayList<>(SIZE);
for (int i = 0; i < SIZE; i++) {
arrayList.add(i);
}
// JIT 최적화 방지 및 GC 영향 제거
int sum = 0;
System.gc();
// HashMap 접근 시간
long startHash = System.nanoTime();
for (int i = 0; i < SIZE; i++) {
sum += hashMap.get(i); // 최적화 방지
}
long endHash = System.nanoTime();
System.out.println("HashMap 조회 시간(ns): \t\t" + (endHash - startHash));
// TreeMap 접근 시간
long startTree = System.nanoTime();
for (int i = 0; i < SIZE; i++) {
sum += treeMap.get(i); // 최적화 방지
}
long endTree = System.nanoTime();
System.out.println("TreeMap 조회 시간(ns): \t\t" + (endTree - startTree) +
" (logN: " + String.format("%.2f", Math.log(SIZE) / Math.log(2)) + ")");
// ArrayList 접근 시간
long startList = System.nanoTime();
for (int i = 0; i < SIZE; i++) {
sum += arrayList.get(i); // 최적화 방지
}
long endList = System.nanoTime();
System.out.println("ArrayList 조회 시간(ns): \t" + (endList - startList));
// 결과 확인
System.out.println("검증용 sum 값: " + sum);
System.out.println();
}
}
}ArrayList 접근 시간은 gc나 JIT 컴파일러로 인한 오버헤드나 최적화 등을 고려해서 코드를 구성했다.

TreeMap이 HashMap 에 비해서 터무니없이 느릴수 있다 생각할수 있지만 테스트 1의 경우를 미루어 보면 최악의 HashMap(충돌)에 비해서는 평균적으로 준수한 성능을 낸다.
- ArrayList (O(1))
- 단순한 배열 인덱스 접근 → 캐시 친화적 & 빠름
- 데이터 크기 증가해도 성능 저하 거의 없음.
- HashMap (O(1) 평균, O(n) 최악)
- 일반적으로 해시 충돌이 적으면 빠름.
- 충돌이 많아질수록 성능이 저하될 가능성이 있음.
- TreeMap (O(log n))
- 내부적으로 Red-Black Tree(균형 이진 탐색 트리) 사용.
- 조회 성능이 항상 O(log n)으로 유지됨.
- 데이터 크기가 커질수록 HashMap보다 느리지만, 최악의 경우에는 HashMap보다 안정적인 성능을 유지.
그래서 언제 뭘 써야하나?
- 데이터 크기가 작을 때
- HashMap > TreeMap (둘 다 빠름)
- ArrayList는 인덱스 조회용으로 유리
- 데이터 크기가 클 때
- TreeMap은 항상 O(log n), 성능이 일정하지만 HashMap보다 느림.
- HashMap은 충돌이 많으면 TreeMap보다 더 느려질 수 있음.
- ArrayList는 조회가 많을 때 가장 빠름.
- 정렬이 필요하면?
- TreeMap은 정렬된 데이터를 유지하므로 탐색이 빈번한 경우에는 유용.
4. 해결책 또는 예방법
- 입력 데이터 특성 파악
- TreeMap 활용
- HashMap 최적화 파라미터 조정
- 참조 지역성 개선
이라고 제시를 해주고 있지만 코드포스나 자유게시판의 글을 확인 해보면
- 데이터가 지나치게 많거나(예: 수천만 건 이상),
- 해시 저격 패턴(Adversarial input)이 의심될 때,
- N^2 루프만으로도 충분히 시간을 먹을 때,
- 해시의 상수 오버헤드나 최악 상황이 부담스러울 때,
- 이럴 땐 정렬+이분 탐색(O(N^2 log N)), 투 포인터, 혹은 다른 자료구조(Map, TreeMap, Segment Tree 등)를 고려한다.
위의 경우에는 사용을 하지 않는걸 추천한다고 한다.
마무리
그럼 우리는 어떻게 이런 상황을 해결하거나 예방해야할까?
- 입력 데이터 특성 파악
- 키가 특정 패턴으로 몰리지 않도록, 혹은 악의적 패턴을 방어하고 싶다면 커스텀 해시 함수를 강화(더 균등하게)하거나,
- 해싱 대신 정렬 + 이분 탐색(TreeMap, Arrays.binarySearch 등) 같은 다른 알고리즘을 검토한다.
- TreeMap 활용
- 항상 O(log N) 복잡도이며, 해시 충돌 걱정을 덜 수 있다.
- 다만 평균적으로 HashMap보다는 상수 시간 비용이 크다.
- HashMap 최적화 파라미터
- 초기 용량(capacity)을 여유롭게 잡고, 적절한 부하율(load factor)을 설정하면 재해시(rehash) 횟수를 줄일 수 있다.
- 그러나 해시 충돌 입력 자체를 해결하진 못한다.
- 참조 지역성 개선
- 객체 접근이 분산되지 않도록, 자료구조 선택 시 연속적 메모리를 최대한 활용하면 캐시 효율이 올라간다(예: 배열, ArrayList).
- 해시맵이 불가피하다면, 무작정 큰 N 데이터가 들어오지 않도록 제한을 두거나, 다른 알고리즘으로 문제를 풀 수 있는지 고려한다.
'Java' 카테고리의 다른 글
| 조건문 없이 깔끔하게, 자바 비트마스킹으로 문제 해결하는 법 (사용 유형 정리) (0) | 2025.03.04 |
|---|---|
| 자바8 람다와 함수형 인터페이스 [3] : 디슈거링을 통한 메서드 변환과 MethodHandle, 바이트코드/JVM 분석 (1) | 2025.02.11 |
| 자바8 람다와 함수형 인터페이스 [2] : @FunctionalInterface 구현체 작성법(람다 표현식) (0) | 2025.02.11 |
| 자바8 람다와 함수형 인터페이스 [1] : 람다의 등장 배경 (0) | 2025.02.11 |
| JAVA 문법 QUIZ [2] (2) | 2025.02.04 |
