목차
알고리즘 수업 - 피보나치 수 1(#24416)
- Problem
오늘도 서준이는 동적 프로그래밍 수업 조교를 하고 있다. 아빠가 수업한 내용을 학생들이 잘 이해했는지 문제를 통해서 확인해보자. 오늘은 n의 피보나치 수를 재귀호출과 동적 프로그래밍으로 구하는 알고리즘을 배웠다. 재귀호출에 비해 동적 프로그래밍이 얼마나 빠른지 확인해 보자. 아래 의사 코드를 이용하여 n의 피보나치 수를 구할 경우 코드1 코드2 실행 횟수를 출력하자. 피보나치 수 재귀호출 의사 코드는 다음과 같다. fib(n) { if (n = 1 or n = 2) then return 1; # 코드1 else return (fib(n - 1) + fib(n - 2)); } 피보나치 수 동적 프로그래밍 의사 코드는 다음과 같다. fibonacci(n) { f[1] <- f[2] <- 1; for i <- 3 to n f[i] <- f[i - 1] + f[i - 2]; # 코드2 return f[n]; }
- Hint
재귀가 많이 반복될것 같으면 PyPy3로 바꾸어서 제출하자
- Solution
재귀와 Top-down 방식의 동적 트래킹을 이용한 풀이
cntrec = 0
cnt = 0
def fiborec(n):
global cntrec
if n == 0 or n == 1:
cntrec += 1
return cntrec
else:
fiborec(n-1)+fiborec(n-2)
return cntrec
def fibo(n):
global cnt
if fibonum[n] != 0:
return cnt
fibonum[n] = fibo(n-1)+fibo(n-2)
cnt += 1
return cnt
n = int(input())
fibonum = [0]*n
fibonum[0] = 1
fibonum[1] = 1
print(fiborec(n-1), fibo(n-1)-1)재귀는 반복 횟수만 출력한다고 가정했을시에 cnt 변수를 따로 사용하지 않고도 출력이 가능하다.
cnt = 0
def fiborec(n):
if n == 0 or n == 1:
return 1
else:
return fiborec(n-1)+fiborec(n-2)
def fibo(n):
global cnt
if fibonum[n] != 0:
return cnt
fibonum[n] = fibo(n-1)+fibo(n-2)
cnt += 1
return cnt
n = int(input())
fibonum = [0]*n
fibonum[0] = 1
fibonum[1] = 1
print(fiborec(n-1), fibo(n-1)-1)
신나는 함수 실행(#9184)
- Problem
재귀 호출만 생각하면 신이 난다! 아닌가요? 다음과 같은 재귀함수 w(a, b, c)가 있다. if a <= 0 or b <= 0 or c <= 0, then w(a, b, c) returns: 1 if a > 20 or b > 20 or c > 20, then w(a, b, c) returns: w(20, 20, 20) if a < b and b < c, then w(a, b, c) returns: w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c) otherwise it returns: w(a-1, b, c) + w(a-1, b-1, c) + w(a-1, b, c-1) - w(a-1, b-1, c-1) 위의 함수를 구현하는 것은 매우 쉽다. 하지만, 그대로 구현하면 값을 구하는데 매우 오랜 시간이 걸린다. (예를 들면, a=15, b=15, c=15) a, b, c가 주어졌을 때, w(a, b, c)를 출력하는 프로그램을 작성하시오.
- Hint
깊은 복사 얕은 복사에 대해서 알아보자
- Solution
하드카피를 이용한 풀이
def w(a, b, c):
if a <= 0 or b <= 0 or c <= 0:
return 1
elif a > 20 or b > 20 or c > 20:
return w(20, 20, 20)
elif stg[a][b][c] != 0:
return stg[a][b][c]
elif a < b and b < c:
stg[a][b][c] = w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c)
return stg[a][b][c]
else:
stg[a][b][c] = w(a-1, b, c) + w(a-1, b-1, c) + \
w(a-1, b, c-1) - w(a-1, b-1, c-1)
return stg[a][b][c]
result = []
stg = [[[0]*(21) for _ in range(21)] for _ in range(21)]
i = 0
while i == 0:
a, b, c = map(int, input().split())
if a == -1 and b == -1 and c == -1:
i = 1
else:
result.append(f'w({a}, {b}, {c}) = {w(a,b,c)}')
print(*result, sep='\n')
하드 카피를 하지 못하였을때의 문제점
stg = [[[None]*21]*21]*21
i = 0
while i == 0:
a, b, c = map(int, input().split())
if a == -1 and b == -1 and c == -1:
i = 1
print(f'w({a}, {b}, {c}) = {w(a,b,c)}')위에 있는 하드카피로 성공하기 전에 실패했던 방법
단순하게 nested list 형식으로 21을 곱해주었다. 얕은 복사와 깊은 복사의 개념을 알지 못했고 혹시나 해서 리스트를 프린트 해서
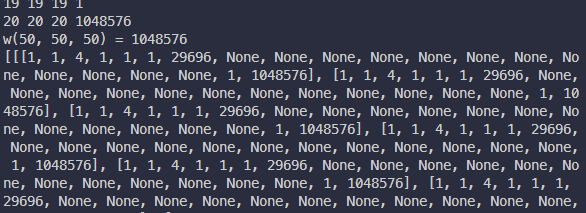
위와같은 결과값이 나와서 제대로 리스트에 추가가 되지 않고 있구나 알고 있었지만 왜 그런지는 몰랐다.. 뭐 항상ㅋㅋ
이에 대한 포스팅
2022.10.12 - [BOJ/Indiviual solve] - [백준 9184번, Python] 깊은 복사,얕은 복사 개념
[백준 9184번, Python] 깊은 복사,얕은 복사 개념
신나는 함수 실행(#9184) Problem 재귀 호출만 생각하면 신이 난다! 아닌가요? 다음과 같은 재귀함수 w(a, b, c)가 있다. if a <= 0 or b <= 0 or c <= 0, then w(a, b, c) returns: 1 if a > 20 or b > 20 or c >..
nstgic3.tistory.com
01타일(#1904)
- Problem
지원이에게 2진 수열을 가르쳐 주기 위해, 지원이 아버지는 그에게 타일들을 선물해주셨다. 그리고 이 각각의 타일들은 0 또는 1이 쓰여 있는 낱장의 타일들이다. 어느 날 짓궂은 동주가 지원이의 공부를 방해하기 위해 0이 쓰여진 낱장의 타일들을 붙여서 한 쌍으로 이루어진 00 타일들을 만들었다. 결국 현재 1 하나만으로 이루어진 타일 또는 0타일을 두 개 붙인 한 쌍의 00타일들만이 남게 되었다. 그러므로 지원이는 타일로 더 이상 크기가 N인 모든 2진 수열을 만들 수 없게 되었다. 예를 들어, N=1일 때 1만 만들 수 있고, N=2일 때는 00, 11을 만들 수 있다. (01, 10은 만들 수 없게 되었다.) 또한 N=4일 때는 0011, 0000, 1001, 1100, 1111 등 총 5개의 2진 수열을 만들 수 있다. 우리의 목표는 N이 주어졌을 때 지원이가 만들 수 있는 모든 가짓수를 세는 것이다. 단 타일들은 무한히 많은 것으로 가정하자.
- Hint
Bottom up 방식과 왜 정수를 나누라고 하는지 생각해보자.
점화식을 이용해 규칙을 찾아보자
- Solution
Bottom up 과 메모리 초과를 고려한 풀이
n = int(input())
res = [0]*1000001
res[0] = 1
res[1] = 1
for i in range(2, n+1):
res[i] = res[i-1]+res[i-2]
res[i] = res[i] % 15746
print(res[n])피보나치 수열임을 찾아 주는게 중요하다.
파도반 수열(#9461)
- Problem
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다. 파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다. N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
- Hint
피보나치 수열처럼 이전 번째의 항끼리의 합으로 결과값이 나온다.
- Solution
Bottom up 방식의 동적할당을 이용한 풀이
res = []
pado = [0, 1, 1, 1, 2, 2, 3]
for i in range(7, 101):
pado.append(pado[i-1]+pado[i-5])
n = int(input())
for i in range(n):
a = int(input())
res.append(pado[a])
print(*res, sep='\n')
4칸의 텀을 두고
pado[i]=pado[i-1]+pado[i-5]이러한 구조를 가지고 있기에 위와같이 풀이하였다.
연속합(#1912)
- Problem
n개의 정수로 이루어진 임의의 수열이 주어진다. 우리는 이 중 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 합을 구하려고 한다. 단, 수는 한 개 이상 선택해야 한다. 예를 들어서 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 이라는 수열이 주어졌다고 하자. 여기서 정답은 12+21인 33이 정답이 된다.
- Solution
import sys
input()
dp=[-1000]
cnt=0
for n in sys.stdin.readline().split():
dp.append(max(int(dp[cnt])+int(n),int(n)))
cnt+=1
print(max(dp))
다음에 오는 숫자가 음수만 아니라면 더해주어도 상관이 없다. 처음에는 부호를 if 로 구별하고 더하려고 하다가 이를 max(n,0) 으로 표현하면 깔끔하게 표현된다는 스킬을 배웠다.
리스트에 저장하여 max 로 꺼내는 방식이 생각보다 오래 걸리지 않았다. 둘다 Bottom up 방식이라 그런것 같다.
RGB거리(#1149)
- Problem
RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다. 집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자. 1번 집의 색은 2번 집의 색과 같지 않아야 한다. N번 집의 색은 N-1번 집의 색과 같지 않아야 한다. i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.
- Solution
import sys
n = int(input())
dp=[]
for m in range(n):
dp.append(list(map(int,input().split())))
for i in range(n-1):
dp[i+1][0] = min(dp[i][1],dp[i][2])+dp[i+1][0]
dp[i+1][1] = min(dp[i][0],dp[i][2])+dp[i+1][1]
dp[i+1][2] = min(dp[i][0],dp[i][1])+dp[i+1][2]
print(min(dp[i+1][0],dp[i+1][1],dp[i+1][2]))
동적 계획법은 재귀를 이용하는 Top down 방식이 아니라 Down up 방식이다. 또한 새로운 리스트를 만들지 않고 할당되었던 리스트의 위치를 재활용해서 사용하는 방식을 취하고 있다. 위의 식에서 보게된다면 [i+1]의 값을 재할당 해주고 있는데 이는 그 줄에서 최소의 비용을 가지는 경우를 계산해서 넣어주는 것이다. 쉽게 말해 두번째 줄의 첫번째 경우를 선택하였을때 그 이전 줄이었던 첫번째 줄 중 최소값을 현재 선택한 값과 합을 하여 재할당을 해놓으면 우리는 더이상 for 문에 의해서 반복되었을때 이전 단계에 대한 생각을 할 필요가 없어진다.
- 나의 경우에는 재귀 형식으로 생각을 하다가 풀이가 늦어졌다. 아무래도 앞에서 재귀를 배웠다보니 점화식이 먼저 생각이 든다.
정수 삼각형(#1932)
- Problem
7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 위 그림은 크기가 5인 정수 삼각형의 한 모습이다. 맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다. 삼각형의 크기는 1 이상 500 이하이다. 삼각형을 이루고 있는 각 수는 모두 정수이며, 범위는 0 이상 9999 이하이다.
- Solution
import sys
n = int(input())
dp=[]
for m in range(n):
dp.append([0]+list(map(int,input().split()))+[0])
for i in range(1,n):
for j in range(1,i+2):
dp[i][j] = max(dp[i-1][j-1],dp[i-1][j])+dp[i][j]
print(max(dp[n-1]))
print(dp)
RGB거리에서 설명했던 내용대로 이전 단계의 값을 계산하여 현 단계에 가중치를 더하는 방식으로 풀이를 가져갔다. RGB거리와 다른 점은 위 거리는 단계마다 항목의 개수가 변하지 않는 구조이지만 이 문제는 피라미드 형태로 단계가 증가할수록 항목이 1개 씩 늘어나는 구조이다. 따라서 동적계획법으로 짜기 위해서는 반복문이 진행되면서 원하는 리스트의 원소를 선택할 수 있는 점화식을 짜는것이 중요했다. 따라서 모든 리스트의 앞뒤에 0을 하나씩 넣어주어서 List index error 를 회피하였다.
계단 오르기(#2579)
- Problem
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다. <그림 1> 예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다. <그림 2> 계단 오르는 데는 다음과 같은 규칙이 있다. 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다. 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다. 마지막 도착 계단은 반드시 밟아야 한다. 따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다. 각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
- Solution
n = int(input())
dp=[]
for m in range(n):
dp.append(int(input()))
res =[0]*(n+1)
res[1]=dp[0]
if n>=2:
res[2]=dp[0]+dp[1]
for i in range(2,n):
res[i+1]+=max(dp[i-1]+res[i-2],res[i-1])+dp[i]
print(res[n])
처음에 아이디어는 잘 잡았지만 생각을 잘못해서 푸는데 오래걸린 문제.. n=1 인 경우를 따로 만들어주면 쉽게 문제가 해결된다. res[i+1]+=max(dp[i-1]+res[i-2],res[i-1])+dp[i] 에서 res를 따로 사용하는 이유가 궁금할 수 있는데 \*res[i-2] 와 dp[i-3]의 리스트 위치가 같다. 바로 이 부분이 연속하여 3개를 선택하지 못하게 하는 트리거이다. 만일 dp 대신 res(이전 값을 고려한 값)을 사용하였을 경우에 res[i+1]+=max(res[i]+res[i-2],res[i-1])+dp[i] 꼴로 변화하게 되는데 이러한 경우 res[i]를 구할때 max()에서 후자의 경우를 골랐다고 가정하는 경우 i+1 , i , i-1 총 세가지가 선택되는 후보가 되기 때문이다.
1로 만들기(#1463)
- Problem
정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지 이다. X가 3으로 나누어 떨어지면, 3으로 나눈다. X가 2로 나누어 떨어지면, 2로 나눈다. 1을 뺀다. 정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.
- Solution
n = int(input())
dp =[0]*(n+1)
dp[1]=0
for i in range(2,n+1):
if i%2==0 and i%3==0:
dp[i]=min(dp[i-1], dp[i//2], dp[i//3])+1
elif i%2==0:
dp[i]=min(dp[i-1], dp[i//2])+1
elif i%3==0:
dp[i]=min(dp[i-1], dp[i//3])+1
else:
dp[i]=dp[i-1]+1
print(dp[-1])
예시로 주어진 10 처럼 1을 뺀 후에 9에 대한 최소 경로로 구하는 방식이 더 짧은 경우가 몇가지 존재한다. 1을 두번 연속하여 빼는 경우는 존재하지 않다. 어떤 경우던지 빼지 않거나 1번만 1을 빼게 되어도 2에 대해서 약분이 되기 때문이다. 따라서 이 문제는 2,3의 공배수일때 2, 3 각각의 배수일때 세 경우다 아닐때를 상정하여 동적 계획법을 이용하여 풀이가 가능하다. 숏코딩에서는 조건이 어떻게 부여되었는지를 확인하여보자 dp[i]=min(dp[i-1], dp[i//2]+i%2, dp[i//3]+i%3)+1
쉬운 계단 수(#10844)
- Problem
45656이란 수를 보자. 이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다. N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.
- Solution
n= int(input())
pd=[[0 for i in range(12)] for j in range(n)]
pd[0]=[0,0,1,1,1,1,1,1,1,1,1,0]
if n>=1:
for i in range(1,n):
for j in range(1,11):
pd[i][j] = int(pd[i-1][j-1])+int(pd[i-1][j+1])
print(sum(pd[n-1])%1000000000)
0111111111 1122222221 1334444432 3578888763 5900000006
처음에는 피보나치 수열인줄 알았지만.. 아니었다. 2번째 자리부터 제한이 풀리는 0도 고려하고 본질적으로는 0과 9의 뒤에 -1 , 10이 올수 없으니 각 경우마다 1개씩 결여가 되는 사실을 이용하여 전 단계의 0과 9의 개수를 계산하게 되면 답을 구할 수 있다. 하지만 9은 8 뒤에 나올수 있고 8은 7 뒤에 ... 따라서 전 자리수를 전부 고려해주어야 별도의 자리수 개수를 구할수 있기에 나열을 하여 규칙을 찾아본다.
포도주 시식(#2156)
- Problem
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규칙이 있다. 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다. 연속으로 놓여 있는 3잔을 모두 마실 수는 없다. 효주는 될 수 있는 대로 많은 양의 포도주를 맛보기 위해서 어떤 포도주 잔을 선택해야 할지 고민하고 있다. 1부터 n까지의 번호가 붙어 있는 n개의 포도주 잔이 순서대로 테이블 위에 놓여 있고, 각 포도주 잔에 들어있는 포도주의 양이 주어졌을 때, 효주를 도와 가장 많은 양의 포도주를 마실 수 있도록 하는 프로그램을 작성하시오. 예를 들어 6개의 포도주 잔이 있고, 각각의 잔에 순서대로 6, 10, 13, 9, 8, 1 만큼의 포도주가 들어 있을 때, 첫 번째, 두 번째, 네 번째, 다섯 번째 포도주 잔을 선택하면 총 포도주 양이 33으로 최대로 마실 수 있다.
- Solution
n = int(input())
pd=[0]*n
each=[]
row=[0]*n
for i in range(n):
each.append(int(input()))
pd[0] = each[0]
if n>1:
pd[1] = each[0]+each[1]
if n>2:
pd[2] = max(each[2]+each[1],each[2]+each[0],pd[1])
for i in range(3,n):
row[i]=each[i]+each[i-1]
pd[i] = max(each[i]+pd[i-2],pd[i-1],row[i]+pd[i-3])
print(pd[0:2])
print(pd[n-1])
규칙을 생각하여 점화식을 만들때 1개, 2개, 3개가 있는 경우에는 각각 2개 까지는 모두 선택하고 3개는 셋중에 최소값을 제외한 2개를 선택할수 밖에 없다. 이후 4개 이상부터는 마지막 와인을 선택하는 경우와 선택하지 않는 경우 또 선택을 한 경우에는 마지막과 그 전 와인 모두를 연속으로 선택하는 경우인지 아니면 마지막만 선택하는 경우인지로 나눌수 있다고 생각이 들어서 pd[i-2] row[i]+pd[i-3] each[i]+pd[i-2] 로 나누어 생각했다.
가장 긴 증가하는 부분 수열(#11053)
- Problem
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
- Solution
# 리스트에 번호를 저장하는 것이 아니라 번호를 index로 1을 저장한다.
n = int(input())
alist=[0]*1001
for i in map(int,input().split()):
alist[i] = max(alist[:i])+1
print(max(alist))
결국에는 인터넷을 찾아가면서 풀게된 문제이다. 처음에는 pd를 [][] 2차원 배열 형식으로 나타내어 0번째에는 주어진 값을 1번째에는 이전까지의 값들을 고려하여 계산된 가중치(1~)에 대해서 나타내어 index를 가져오는 것에 대한 연산을 줄이려고 했었다. 하지만 2차원리스트에 대한 지식도 부족하였을뿐더러 2차원형태의 리스트를 짠다고 하더라도 index에 대한 정보를 2중의 반복문 없이는 가져오는것이 불가능했었고 답을 보기 전에는 안되는 이유가 잘못된 아이디어 때문인지 2차원리스트에 대한 이해도 부족인지에 대해서 알지 못했다. 결론적으로는 index를 얻기 위해서는 2중의 반복문을 수행했어야했고 또한 따로 가중치에 대한 리스트를 정의하여 문제를 해결하는게 더 편했다.
또한 pd[j]=max(pd[k]+1,pd[j]) 부분 또한 +1 을 pd[j]=max(pd[k],pd[j])+1 혹은 pd[j]+=max(pd[k],pd[j]) 등으로 표현하려고 했던것이 착오점이었다.
가장 긴 바이토닉 부분 수열(#11054)
- Problem
수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < ... Sk-1 < Sk > Sk+1 > ... SN-1 > SN을 만족한다면, 그 수열을 바이토닉 수열이라고 한다. 예를 들어, {10, 20, 30, 25, 20}과 {10, 20, 30, 40}, {50, 40, 25, 10} 은 바이토닉 수열이지만, {1, 2, 3, 2, 1, 2, 3, 2, 1}과 {10, 20, 30, 40, 20, 30} 은 바이토닉 수열이 아니다. 수열 A가 주어졌을 때, 그 수열의 부분 수열 중 바이토닉 수열이면서 가장 긴 수열의 길이를 구하는 프로그램을 작성하시오.
- Solution
n = int(input())
alist=list(map(int,input().split()))
rev_alist = alist[::-1]
pdu=[1 for m in range(n)]
pdd=[1 for m in range(n)]
pd=[0]*n
for j in range(1,n):
for k in range(j):
if alist[k]<alist[j]:
pdu[j]=max(pdu[k]+1,pdu[j])
if rev_alist[k]<rev_alist[j]:
pdd[j]=max(pdd[k]+1,pdd[j])
pdd = pdd[::-1]
for l in range(n):
pd[l]=pdu[l]+pdd[l]-1
print(max(pd))
이전 문제인 가장 긴 증가하는 부분 수열 문제를 풀고 이해를 했다면 아이디어는 쉽게 가져올수 있었던것 같다. 하지만 pd에 개수를 채워줄때 이전 pd 값이 필요했기에 단순히 감소하는 부분 수열을 구하기 위해서 앞 부분부터 접근하게 되면 풀이가 되지 않는다. 따라서 리스트의 뒷부분부터 접근하여 계산하기 위한 방법을 생각해보면 되는데 1. 리스트의 위치를 가르키는 인자를 n-i 형식으로 뒤부터 채워지게 한다 2. 리스트를 reverse 시켜서 다시 저장하여 사용한다 이중 2번 방식은 반복문을 한번만 돌리기만 하면 되기때문에 2번 방법을 선택하였다. 또한 중요한 점은 각 수열 길이를 구할때 자기 자신또한 포함한 값을 저장하기 때문에(기본값 1) 마지막 결과값에서 1을 빼주면 좋다.
전깃줄(#2565)
- Problem
두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다. 예를 들어, < 그림 1 >과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다. < 그림 1 > 전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
- Solution
n = int(input())
a={}
alist=[]
# 딕셔너리 형태로 저장
for i in range(n):
k,v = input().split()
a[int(k)] = int(v)
# sorted 와 비슷한 형태
for i in range(1,501):
if i in a:
alist.append(a[i])
# 다만 pd의 리스트 개수를 n개로 데이터 세이브
pd=[1 for m in range(n)]
for j in range(1,n):
for k in range(j):
if alist[k]<alist[j]:
pd[j]=max(pd[k]+1,pd[j])
print(n-max(pd))
8 2 9 1 4 6 7 10
LCS(#9251)
- Problem
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
- Solution
a=list(map(str,input()))
b=list(map(str,input()))
pd = [[0 for n in range(len(b)+1)] for m in range(len(a)+1)]
lcsword = []
for i in range(len(a)):
for j in range(len(b)):
if a[i]==b[j]:
pd[i+1][j+1]=pd[i][j]+1
lcsword.append(a[i])
else:
pd[i+1][j+1]=max(pd[i][j+1],pd[i+1][j])
print(max(map(max,pd)))
print(lcsword)
동적 계획법을 사용하기 위해서는 항상 이전의 경우가 계산된 값을 잘 이용해야된다는 사실을 기반으로 코드의 답을 생각하여야한다. 두 문자열이 항상 같은 길이일수 없는 경우도 생각을 하였을때 결론적으로는 이전 경우들이 저장되는 pd 리스트가 2차원 배열의 형태를 가지고 있어서 [n][m] 인 경우 n번째 까지의 첫번째 문자열과 m번째 까지의 두번째 문자열 사이의 공통부분에 대해서 저장을 하는 아이디어를 가져간다.
평범한 배낭(#12865)
- Problem
이 문제는 아주 평범한 배낭에 관한 문제이다. 한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다. 준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.
- Solution
n, k = map(int,input().split())
pd = [[0 for i in range(k+1)] for j in range(n+1)]
for i in range(1,n+1):
w, v = map(int,input().split())
for j in range(1,k+1):
if j
앞서 풀었던 동적 계획법 문제와는 다른점이 결과값에 영향을 주는 요소들의 순서에 관계가 없다. 포도주, 계단, LIS 문제 등은 요소들 사이에 정렬에 관련된 규칙이 (점점 커지거나 작아지는 순서) 등이 존재하는 반면 LCS나 평범한 배낭 문제는 정렬관련된 규칙이 순서로 존재하는 것이 아니라 어떤 Limit 값을 초과하지 않게 요소들의 합을 구성하는 형태 등으로 나와있다. 따라서 이는 LCS와 마찬가지로 2차원 리스트 수열로 나열하여 풀면 좋을것 같다. 어차피 버틸수 있는 무게를 증가하는 무게에 대해서는 카운트를 할 필요가 없다는 성질을 이용하여 리스트의 한쪽을 무게로 두어주고 각 단계(i)가 변화할때마다 이전의 값들을 이용하여 새로 추가되는 값을 상정한 값을 저장하게 하는 점화식을 찾아본다. 2차원 리스트 수열 형태로의 저장의 장점은 문제를 보고 일차적으로 접근하게 된다면 무게 4와 3이 있을경우 그 둘을 더한 경우만 계산해도되는것이 아닌가? 생각할수 있는데(나도 그렇게 생각했다) 하지만 각각의 경우를 계산하여 리스트에 할당해주는것 보다 2차원 배열 전체를 계산하는 코드를 만들고 이를 실행하기 위한 메모리가 더 적게 쓰이게 된다.
색다른 풀이과정이 궁금하다면 참고하길 바란다.
GitHub - ChoMinGi/BOJ-python
Contribute to ChoMinGi/BOJ-python development by creating an account on GitHub.
github.com
'Baekjoon > Stepbystep' 카테고리의 다른 글
| [백준/python] 그리디 알고리즘 전체 풀이(19단계) (0) | 2023.01.21 |
|---|---|
| [백준/python] 누적 합 전체 풀이(18단계) (0) | 2023.01.17 |
| [백준/python] 백트래킹 전체 풀이(15단계) (0) | 2022.09.26 |
| [백준/python] 정수론 및 조합론 전체 풀이(14단계) (0) | 2022.09.02 |
| [백준/python] 기하 1 전체 풀이(13단계) (1) | 2022.08.31 |
목차
알고리즘 수업 - 피보나치 수 1(#24416)
- Problem
오늘도 서준이는 동적 프로그래밍 수업 조교를 하고 있다. 아빠가 수업한 내용을 학생들이 잘 이해했는지 문제를 통해서 확인해보자. 오늘은 n의 피보나치 수를 재귀호출과 동적 프로그래밍으로 구하는 알고리즘을 배웠다. 재귀호출에 비해 동적 프로그래밍이 얼마나 빠른지 확인해 보자. 아래 의사 코드를 이용하여 n의 피보나치 수를 구할 경우 코드1 코드2 실행 횟수를 출력하자. 피보나치 수 재귀호출 의사 코드는 다음과 같다. fib(n) { if (n = 1 or n = 2) then return 1; # 코드1 else return (fib(n - 1) + fib(n - 2)); } 피보나치 수 동적 프로그래밍 의사 코드는 다음과 같다. fibonacci(n) { f[1] <- f[2] <- 1; for i <- 3 to n f[i] <- f[i - 1] + f[i - 2]; # 코드2 return f[n]; }
- Hint
재귀가 많이 반복될것 같으면 PyPy3로 바꾸어서 제출하자
- Solution
재귀와 Top-down 방식의 동적 트래킹을 이용한 풀이
cntrec = 0
cnt = 0
def fiborec(n):
global cntrec
if n == 0 or n == 1:
cntrec += 1
return cntrec
else:
fiborec(n-1)+fiborec(n-2)
return cntrec
def fibo(n):
global cnt
if fibonum[n] != 0:
return cnt
fibonum[n] = fibo(n-1)+fibo(n-2)
cnt += 1
return cnt
n = int(input())
fibonum = [0]*n
fibonum[0] = 1
fibonum[1] = 1
print(fiborec(n-1), fibo(n-1)-1)재귀는 반복 횟수만 출력한다고 가정했을시에 cnt 변수를 따로 사용하지 않고도 출력이 가능하다.
cnt = 0
def fiborec(n):
if n == 0 or n == 1:
return 1
else:
return fiborec(n-1)+fiborec(n-2)
def fibo(n):
global cnt
if fibonum[n] != 0:
return cnt
fibonum[n] = fibo(n-1)+fibo(n-2)
cnt += 1
return cnt
n = int(input())
fibonum = [0]*n
fibonum[0] = 1
fibonum[1] = 1
print(fiborec(n-1), fibo(n-1)-1)
신나는 함수 실행(#9184)
- Problem
재귀 호출만 생각하면 신이 난다! 아닌가요? 다음과 같은 재귀함수 w(a, b, c)가 있다. if a <= 0 or b <= 0 or c <= 0, then w(a, b, c) returns: 1 if a > 20 or b > 20 or c > 20, then w(a, b, c) returns: w(20, 20, 20) if a < b and b < c, then w(a, b, c) returns: w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c) otherwise it returns: w(a-1, b, c) + w(a-1, b-1, c) + w(a-1, b, c-1) - w(a-1, b-1, c-1) 위의 함수를 구현하는 것은 매우 쉽다. 하지만, 그대로 구현하면 값을 구하는데 매우 오랜 시간이 걸린다. (예를 들면, a=15, b=15, c=15) a, b, c가 주어졌을 때, w(a, b, c)를 출력하는 프로그램을 작성하시오.
- Hint
깊은 복사 얕은 복사에 대해서 알아보자
- Solution
하드카피를 이용한 풀이
def w(a, b, c):
if a <= 0 or b <= 0 or c <= 0:
return 1
elif a > 20 or b > 20 or c > 20:
return w(20, 20, 20)
elif stg[a][b][c] != 0:
return stg[a][b][c]
elif a < b and b < c:
stg[a][b][c] = w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c)
return stg[a][b][c]
else:
stg[a][b][c] = w(a-1, b, c) + w(a-1, b-1, c) + \
w(a-1, b, c-1) - w(a-1, b-1, c-1)
return stg[a][b][c]
result = []
stg = [[[0]*(21) for _ in range(21)] for _ in range(21)]
i = 0
while i == 0:
a, b, c = map(int, input().split())
if a == -1 and b == -1 and c == -1:
i = 1
else:
result.append(f'w({a}, {b}, {c}) = {w(a,b,c)}')
print(*result, sep='\n')
하드 카피를 하지 못하였을때의 문제점
stg = [[[None]*21]*21]*21
i = 0
while i == 0:
a, b, c = map(int, input().split())
if a == -1 and b == -1 and c == -1:
i = 1
print(f'w({a}, {b}, {c}) = {w(a,b,c)}')위에 있는 하드카피로 성공하기 전에 실패했던 방법
단순하게 nested list 형식으로 21을 곱해주었다. 얕은 복사와 깊은 복사의 개념을 알지 못했고 혹시나 해서 리스트를 프린트 해서

위와같은 결과값이 나와서 제대로 리스트에 추가가 되지 않고 있구나 알고 있었지만 왜 그런지는 몰랐다.. 뭐 항상ㅋㅋ
이에 대한 포스팅
2022.10.12 - [BOJ/Indiviual solve] - [백준 9184번, Python] 깊은 복사,얕은 복사 개념
[백준 9184번, Python] 깊은 복사,얕은 복사 개념
신나는 함수 실행(#9184) Problem 재귀 호출만 생각하면 신이 난다! 아닌가요? 다음과 같은 재귀함수 w(a, b, c)가 있다. if a <= 0 or b <= 0 or c <= 0, then w(a, b, c) returns: 1 if a > 20 or b > 20 or c >..
nstgic3.tistory.com
01타일(#1904)
- Problem
지원이에게 2진 수열을 가르쳐 주기 위해, 지원이 아버지는 그에게 타일들을 선물해주셨다. 그리고 이 각각의 타일들은 0 또는 1이 쓰여 있는 낱장의 타일들이다. 어느 날 짓궂은 동주가 지원이의 공부를 방해하기 위해 0이 쓰여진 낱장의 타일들을 붙여서 한 쌍으로 이루어진 00 타일들을 만들었다. 결국 현재 1 하나만으로 이루어진 타일 또는 0타일을 두 개 붙인 한 쌍의 00타일들만이 남게 되었다. 그러므로 지원이는 타일로 더 이상 크기가 N인 모든 2진 수열을 만들 수 없게 되었다. 예를 들어, N=1일 때 1만 만들 수 있고, N=2일 때는 00, 11을 만들 수 있다. (01, 10은 만들 수 없게 되었다.) 또한 N=4일 때는 0011, 0000, 1001, 1100, 1111 등 총 5개의 2진 수열을 만들 수 있다. 우리의 목표는 N이 주어졌을 때 지원이가 만들 수 있는 모든 가짓수를 세는 것이다. 단 타일들은 무한히 많은 것으로 가정하자.
- Hint
Bottom up 방식과 왜 정수를 나누라고 하는지 생각해보자.
점화식을 이용해 규칙을 찾아보자
- Solution
Bottom up 과 메모리 초과를 고려한 풀이
n = int(input())
res = [0]*1000001
res[0] = 1
res[1] = 1
for i in range(2, n+1):
res[i] = res[i-1]+res[i-2]
res[i] = res[i] % 15746
print(res[n])피보나치 수열임을 찾아 주는게 중요하다.
파도반 수열(#9461)
- Problem
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다. 파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다. N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
- Hint
피보나치 수열처럼 이전 번째의 항끼리의 합으로 결과값이 나온다.
- Solution
Bottom up 방식의 동적할당을 이용한 풀이
res = []
pado = [0, 1, 1, 1, 2, 2, 3]
for i in range(7, 101):
pado.append(pado[i-1]+pado[i-5])
n = int(input())
for i in range(n):
a = int(input())
res.append(pado[a])
print(*res, sep='\n')
4칸의 텀을 두고
pado[i]=pado[i-1]+pado[i-5]이러한 구조를 가지고 있기에 위와같이 풀이하였다.
연속합(#1912)
- Problem
n개의 정수로 이루어진 임의의 수열이 주어진다. 우리는 이 중 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 합을 구하려고 한다. 단, 수는 한 개 이상 선택해야 한다. 예를 들어서 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 이라는 수열이 주어졌다고 하자. 여기서 정답은 12+21인 33이 정답이 된다.
- Solution
import sys
input()
dp=[-1000]
cnt=0
for n in sys.stdin.readline().split():
dp.append(max(int(dp[cnt])+int(n),int(n)))
cnt+=1
print(max(dp))
다음에 오는 숫자가 음수만 아니라면 더해주어도 상관이 없다. 처음에는 부호를 if 로 구별하고 더하려고 하다가 이를 max(n,0) 으로 표현하면 깔끔하게 표현된다는 스킬을 배웠다.
리스트에 저장하여 max 로 꺼내는 방식이 생각보다 오래 걸리지 않았다. 둘다 Bottom up 방식이라 그런것 같다.
RGB거리(#1149)
- Problem
RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다. 집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자. 1번 집의 색은 2번 집의 색과 같지 않아야 한다. N번 집의 색은 N-1번 집의 색과 같지 않아야 한다. i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.
- Solution
import sys
n = int(input())
dp=[]
for m in range(n):
dp.append(list(map(int,input().split())))
for i in range(n-1):
dp[i+1][0] = min(dp[i][1],dp[i][2])+dp[i+1][0]
dp[i+1][1] = min(dp[i][0],dp[i][2])+dp[i+1][1]
dp[i+1][2] = min(dp[i][0],dp[i][1])+dp[i+1][2]
print(min(dp[i+1][0],dp[i+1][1],dp[i+1][2]))
동적 계획법은 재귀를 이용하는 Top down 방식이 아니라 Down up 방식이다. 또한 새로운 리스트를 만들지 않고 할당되었던 리스트의 위치를 재활용해서 사용하는 방식을 취하고 있다. 위의 식에서 보게된다면 [i+1]의 값을 재할당 해주고 있는데 이는 그 줄에서 최소의 비용을 가지는 경우를 계산해서 넣어주는 것이다. 쉽게 말해 두번째 줄의 첫번째 경우를 선택하였을때 그 이전 줄이었던 첫번째 줄 중 최소값을 현재 선택한 값과 합을 하여 재할당을 해놓으면 우리는 더이상 for 문에 의해서 반복되었을때 이전 단계에 대한 생각을 할 필요가 없어진다.
- 나의 경우에는 재귀 형식으로 생각을 하다가 풀이가 늦어졌다. 아무래도 앞에서 재귀를 배웠다보니 점화식이 먼저 생각이 든다.
정수 삼각형(#1932)
- Problem
7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 위 그림은 크기가 5인 정수 삼각형의 한 모습이다. 맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다. 삼각형의 크기는 1 이상 500 이하이다. 삼각형을 이루고 있는 각 수는 모두 정수이며, 범위는 0 이상 9999 이하이다.
- Solution
import sys
n = int(input())
dp=[]
for m in range(n):
dp.append([0]+list(map(int,input().split()))+[0])
for i in range(1,n):
for j in range(1,i+2):
dp[i][j] = max(dp[i-1][j-1],dp[i-1][j])+dp[i][j]
print(max(dp[n-1]))
print(dp)
RGB거리에서 설명했던 내용대로 이전 단계의 값을 계산하여 현 단계에 가중치를 더하는 방식으로 풀이를 가져갔다. RGB거리와 다른 점은 위 거리는 단계마다 항목의 개수가 변하지 않는 구조이지만 이 문제는 피라미드 형태로 단계가 증가할수록 항목이 1개 씩 늘어나는 구조이다. 따라서 동적계획법으로 짜기 위해서는 반복문이 진행되면서 원하는 리스트의 원소를 선택할 수 있는 점화식을 짜는것이 중요했다. 따라서 모든 리스트의 앞뒤에 0을 하나씩 넣어주어서 List index error 를 회피하였다.
계단 오르기(#2579)
- Problem
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다. <그림 1> 예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다. <그림 2> 계단 오르는 데는 다음과 같은 규칙이 있다. 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다. 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다. 마지막 도착 계단은 반드시 밟아야 한다. 따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다. 각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
- Solution
n = int(input())
dp=[]
for m in range(n):
dp.append(int(input()))
res =[0]*(n+1)
res[1]=dp[0]
if n>=2:
res[2]=dp[0]+dp[1]
for i in range(2,n):
res[i+1]+=max(dp[i-1]+res[i-2],res[i-1])+dp[i]
print(res[n])
처음에 아이디어는 잘 잡았지만 생각을 잘못해서 푸는데 오래걸린 문제.. n=1 인 경우를 따로 만들어주면 쉽게 문제가 해결된다. res[i+1]+=max(dp[i-1]+res[i-2],res[i-1])+dp[i] 에서 res를 따로 사용하는 이유가 궁금할 수 있는데 \*res[i-2] 와 dp[i-3]의 리스트 위치가 같다. 바로 이 부분이 연속하여 3개를 선택하지 못하게 하는 트리거이다. 만일 dp 대신 res(이전 값을 고려한 값)을 사용하였을 경우에 res[i+1]+=max(res[i]+res[i-2],res[i-1])+dp[i] 꼴로 변화하게 되는데 이러한 경우 res[i]를 구할때 max()에서 후자의 경우를 골랐다고 가정하는 경우 i+1 , i , i-1 총 세가지가 선택되는 후보가 되기 때문이다.
1로 만들기(#1463)
- Problem
정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지 이다. X가 3으로 나누어 떨어지면, 3으로 나눈다. X가 2로 나누어 떨어지면, 2로 나눈다. 1을 뺀다. 정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.
- Solution
n = int(input())
dp =[0]*(n+1)
dp[1]=0
for i in range(2,n+1):
if i%2==0 and i%3==0:
dp[i]=min(dp[i-1], dp[i//2], dp[i//3])+1
elif i%2==0:
dp[i]=min(dp[i-1], dp[i//2])+1
elif i%3==0:
dp[i]=min(dp[i-1], dp[i//3])+1
else:
dp[i]=dp[i-1]+1
print(dp[-1])
예시로 주어진 10 처럼 1을 뺀 후에 9에 대한 최소 경로로 구하는 방식이 더 짧은 경우가 몇가지 존재한다. 1을 두번 연속하여 빼는 경우는 존재하지 않다. 어떤 경우던지 빼지 않거나 1번만 1을 빼게 되어도 2에 대해서 약분이 되기 때문이다. 따라서 이 문제는 2,3의 공배수일때 2, 3 각각의 배수일때 세 경우다 아닐때를 상정하여 동적 계획법을 이용하여 풀이가 가능하다. 숏코딩에서는 조건이 어떻게 부여되었는지를 확인하여보자 dp[i]=min(dp[i-1], dp[i//2]+i%2, dp[i//3]+i%3)+1
쉬운 계단 수(#10844)
- Problem
45656이란 수를 보자. 이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다. N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.
- Solution
n= int(input())
pd=[[0 for i in range(12)] for j in range(n)]
pd[0]=[0,0,1,1,1,1,1,1,1,1,1,0]
if n>=1:
for i in range(1,n):
for j in range(1,11):
pd[i][j] = int(pd[i-1][j-1])+int(pd[i-1][j+1])
print(sum(pd[n-1])%1000000000)
0111111111 1122222221 1334444432 3578888763 5900000006
처음에는 피보나치 수열인줄 알았지만.. 아니었다. 2번째 자리부터 제한이 풀리는 0도 고려하고 본질적으로는 0과 9의 뒤에 -1 , 10이 올수 없으니 각 경우마다 1개씩 결여가 되는 사실을 이용하여 전 단계의 0과 9의 개수를 계산하게 되면 답을 구할 수 있다. 하지만 9은 8 뒤에 나올수 있고 8은 7 뒤에 ... 따라서 전 자리수를 전부 고려해주어야 별도의 자리수 개수를 구할수 있기에 나열을 하여 규칙을 찾아본다.
포도주 시식(#2156)
- Problem
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규칙이 있다. 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다. 연속으로 놓여 있는 3잔을 모두 마실 수는 없다. 효주는 될 수 있는 대로 많은 양의 포도주를 맛보기 위해서 어떤 포도주 잔을 선택해야 할지 고민하고 있다. 1부터 n까지의 번호가 붙어 있는 n개의 포도주 잔이 순서대로 테이블 위에 놓여 있고, 각 포도주 잔에 들어있는 포도주의 양이 주어졌을 때, 효주를 도와 가장 많은 양의 포도주를 마실 수 있도록 하는 프로그램을 작성하시오. 예를 들어 6개의 포도주 잔이 있고, 각각의 잔에 순서대로 6, 10, 13, 9, 8, 1 만큼의 포도주가 들어 있을 때, 첫 번째, 두 번째, 네 번째, 다섯 번째 포도주 잔을 선택하면 총 포도주 양이 33으로 최대로 마실 수 있다.
- Solution
n = int(input())
pd=[0]*n
each=[]
row=[0]*n
for i in range(n):
each.append(int(input()))
pd[0] = each[0]
if n>1:
pd[1] = each[0]+each[1]
if n>2:
pd[2] = max(each[2]+each[1],each[2]+each[0],pd[1])
for i in range(3,n):
row[i]=each[i]+each[i-1]
pd[i] = max(each[i]+pd[i-2],pd[i-1],row[i]+pd[i-3])
print(pd[0:2])
print(pd[n-1])
규칙을 생각하여 점화식을 만들때 1개, 2개, 3개가 있는 경우에는 각각 2개 까지는 모두 선택하고 3개는 셋중에 최소값을 제외한 2개를 선택할수 밖에 없다. 이후 4개 이상부터는 마지막 와인을 선택하는 경우와 선택하지 않는 경우 또 선택을 한 경우에는 마지막과 그 전 와인 모두를 연속으로 선택하는 경우인지 아니면 마지막만 선택하는 경우인지로 나눌수 있다고 생각이 들어서 pd[i-2] row[i]+pd[i-3] each[i]+pd[i-2] 로 나누어 생각했다.
가장 긴 증가하는 부분 수열(#11053)
- Problem
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
- Solution
# 리스트에 번호를 저장하는 것이 아니라 번호를 index로 1을 저장한다.
n = int(input())
alist=[0]*1001
for i in map(int,input().split()):
alist[i] = max(alist[:i])+1
print(max(alist))
결국에는 인터넷을 찾아가면서 풀게된 문제이다. 처음에는 pd를 [][] 2차원 배열 형식으로 나타내어 0번째에는 주어진 값을 1번째에는 이전까지의 값들을 고려하여 계산된 가중치(1~)에 대해서 나타내어 index를 가져오는 것에 대한 연산을 줄이려고 했었다. 하지만 2차원리스트에 대한 지식도 부족하였을뿐더러 2차원형태의 리스트를 짠다고 하더라도 index에 대한 정보를 2중의 반복문 없이는 가져오는것이 불가능했었고 답을 보기 전에는 안되는 이유가 잘못된 아이디어 때문인지 2차원리스트에 대한 이해도 부족인지에 대해서 알지 못했다. 결론적으로는 index를 얻기 위해서는 2중의 반복문을 수행했어야했고 또한 따로 가중치에 대한 리스트를 정의하여 문제를 해결하는게 더 편했다.
또한 pd[j]=max(pd[k]+1,pd[j]) 부분 또한 +1 을 pd[j]=max(pd[k],pd[j])+1 혹은 pd[j]+=max(pd[k],pd[j]) 등으로 표현하려고 했던것이 착오점이었다.
가장 긴 바이토닉 부분 수열(#11054)
- Problem
수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < ... Sk-1 < Sk > Sk+1 > ... SN-1 > SN을 만족한다면, 그 수열을 바이토닉 수열이라고 한다. 예를 들어, {10, 20, 30, 25, 20}과 {10, 20, 30, 40}, {50, 40, 25, 10} 은 바이토닉 수열이지만, {1, 2, 3, 2, 1, 2, 3, 2, 1}과 {10, 20, 30, 40, 20, 30} 은 바이토닉 수열이 아니다. 수열 A가 주어졌을 때, 그 수열의 부분 수열 중 바이토닉 수열이면서 가장 긴 수열의 길이를 구하는 프로그램을 작성하시오.
- Solution
n = int(input())
alist=list(map(int,input().split()))
rev_alist = alist[::-1]
pdu=[1 for m in range(n)]
pdd=[1 for m in range(n)]
pd=[0]*n
for j in range(1,n):
for k in range(j):
if alist[k]<alist[j]:
pdu[j]=max(pdu[k]+1,pdu[j])
if rev_alist[k]<rev_alist[j]:
pdd[j]=max(pdd[k]+1,pdd[j])
pdd = pdd[::-1]
for l in range(n):
pd[l]=pdu[l]+pdd[l]-1
print(max(pd))
이전 문제인 가장 긴 증가하는 부분 수열 문제를 풀고 이해를 했다면 아이디어는 쉽게 가져올수 있었던것 같다. 하지만 pd에 개수를 채워줄때 이전 pd 값이 필요했기에 단순히 감소하는 부분 수열을 구하기 위해서 앞 부분부터 접근하게 되면 풀이가 되지 않는다. 따라서 리스트의 뒷부분부터 접근하여 계산하기 위한 방법을 생각해보면 되는데 1. 리스트의 위치를 가르키는 인자를 n-i 형식으로 뒤부터 채워지게 한다 2. 리스트를 reverse 시켜서 다시 저장하여 사용한다 이중 2번 방식은 반복문을 한번만 돌리기만 하면 되기때문에 2번 방법을 선택하였다. 또한 중요한 점은 각 수열 길이를 구할때 자기 자신또한 포함한 값을 저장하기 때문에(기본값 1) 마지막 결과값에서 1을 빼주면 좋다.
전깃줄(#2565)
- Problem
두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다. 예를 들어, < 그림 1 >과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다. < 그림 1 > 전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
- Solution
n = int(input())
a={}
alist=[]
# 딕셔너리 형태로 저장
for i in range(n):
k,v = input().split()
a[int(k)] = int(v)
# sorted 와 비슷한 형태
for i in range(1,501):
if i in a:
alist.append(a[i])
# 다만 pd의 리스트 개수를 n개로 데이터 세이브
pd=[1 for m in range(n)]
for j in range(1,n):
for k in range(j):
if alist[k]<alist[j]:
pd[j]=max(pd[k]+1,pd[j])
print(n-max(pd))
8 2 9 1 4 6 7 10
LCS(#9251)
- Problem
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
- Solution
a=list(map(str,input()))
b=list(map(str,input()))
pd = [[0 for n in range(len(b)+1)] for m in range(len(a)+1)]
lcsword = []
for i in range(len(a)):
for j in range(len(b)):
if a[i]==b[j]:
pd[i+1][j+1]=pd[i][j]+1
lcsword.append(a[i])
else:
pd[i+1][j+1]=max(pd[i][j+1],pd[i+1][j])
print(max(map(max,pd)))
print(lcsword)
동적 계획법을 사용하기 위해서는 항상 이전의 경우가 계산된 값을 잘 이용해야된다는 사실을 기반으로 코드의 답을 생각하여야한다. 두 문자열이 항상 같은 길이일수 없는 경우도 생각을 하였을때 결론적으로는 이전 경우들이 저장되는 pd 리스트가 2차원 배열의 형태를 가지고 있어서 [n][m] 인 경우 n번째 까지의 첫번째 문자열과 m번째 까지의 두번째 문자열 사이의 공통부분에 대해서 저장을 하는 아이디어를 가져간다.
평범한 배낭(#12865)
- Problem
이 문제는 아주 평범한 배낭에 관한 문제이다. 한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다. 준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.
- Solution
n, k = map(int,input().split())
pd = [[0 for i in range(k+1)] for j in range(n+1)]
for i in range(1,n+1):
w, v = map(int,input().split())
for j in range(1,k+1):
if j
앞서 풀었던 동적 계획법 문제와는 다른점이 결과값에 영향을 주는 요소들의 순서에 관계가 없다. 포도주, 계단, LIS 문제 등은 요소들 사이에 정렬에 관련된 규칙이 (점점 커지거나 작아지는 순서) 등이 존재하는 반면 LCS나 평범한 배낭 문제는 정렬관련된 규칙이 순서로 존재하는 것이 아니라 어떤 Limit 값을 초과하지 않게 요소들의 합을 구성하는 형태 등으로 나와있다. 따라서 이는 LCS와 마찬가지로 2차원 리스트 수열로 나열하여 풀면 좋을것 같다. 어차피 버틸수 있는 무게를 증가하는 무게에 대해서는 카운트를 할 필요가 없다는 성질을 이용하여 리스트의 한쪽을 무게로 두어주고 각 단계(i)가 변화할때마다 이전의 값들을 이용하여 새로 추가되는 값을 상정한 값을 저장하게 하는 점화식을 찾아본다. 2차원 리스트 수열 형태로의 저장의 장점은 문제를 보고 일차적으로 접근하게 된다면 무게 4와 3이 있을경우 그 둘을 더한 경우만 계산해도되는것이 아닌가? 생각할수 있는데(나도 그렇게 생각했다) 하지만 각각의 경우를 계산하여 리스트에 할당해주는것 보다 2차원 배열 전체를 계산하는 코드를 만들고 이를 실행하기 위한 메모리가 더 적게 쓰이게 된다.
색다른 풀이과정이 궁금하다면 참고하길 바란다.
GitHub - ChoMinGi/BOJ-python
Contribute to ChoMinGi/BOJ-python development by creating an account on GitHub.
github.com
'Baekjoon > Stepbystep' 카테고리의 다른 글
| [백준/python] 그리디 알고리즘 전체 풀이(19단계) (0) | 2023.01.21 |
|---|---|
| [백준/python] 누적 합 전체 풀이(18단계) (0) | 2023.01.17 |
| [백준/python] 백트래킹 전체 풀이(15단계) (0) | 2022.09.26 |
| [백준/python] 정수론 및 조합론 전체 풀이(14단계) (0) | 2022.09.02 |
| [백준/python] 기하 1 전체 풀이(13단계) (1) | 2022.08.31 |
