목차
개요
unconstrained(비구속 최적화)와 constrained optimization(구속 최적화)
그리고 제약의 분류인 equality(등식 제약)와 inequality constraint(부등식 제약)에 대해 알아보자
Unconstrained Optimization; 제약이 없는 최적화
문제의 해결 방법에서 제약 조건이 없는 최적화를 의미
목적 함수(objective function)를 최대화하거나 최소화하는 변수의 값을 찾는 것이 목표입니다.
예를 들어, 어떤 기업이 이익을 최대화하는 생산량을 찾고자 한다면, 이익 함수를 최대화하는 생산량 값을 찾는 것이 unconstrained optimization 문제가 됩니다.
하지만 대부분의 ML에서는 비구속 최적화를 실행하기 보다는 구속 최적화를 실행하기에 개념 이해만 하면된다.
제약이 없는 최적화는 보통 미분을 사용해 해결할 수 있다. 최대값이건 최소값이건 제한 조건이 없기 때문에 목적 함수를 변수에 대해 미분하여 그 기울기가 0이 되는 점을 찾게 된다면 찾을 수 있다.
constrained optimization; 제약이 있는 최적화
목적 함수를 최대화하거나 최소화하는 동시에 일정한 제약 조건을 만족해야 하는 최적화
제약 조건은 equality constraint(등식 제약)과 inequality constraint(부등식 제약)로 구분할 수 있다.
Equality Constraint (등식 제약)
등식 제약은 최적화 문제에서 변수들 사이에 주어진 관계를 나타내는 등식.
예를 들어, 어떤 기업이 이익을 최대화하는 생산량을 찾고자 하는데, 제품 A와 제품 B의 생산량의 합이 정해져 있다면(=) 이러한 제약 조건은 equality constraint로 볼 수 있다.
Inequality Constraint (부등식 제약)
부등식 제약은 최적화 문제에서 변수들 사이에 주어진 관계를 나타내는 부등식.
예를 들어, 어떤 기업이 이익을 최대화하는 생산량을 찾고자 하는데, 제품 A의 생산량이 제품 B의 생산량보다 크거나 같아야 한다면(>=) 이러한 제약 조건은 inequality constraint로 볼 수 있다.
제약이 있는 최적화에서는 일반적으로 라그랑주 승수법(Lagrange Multipliers) 등의 기법을 사용하여 해결한다.
라그랑주 승수법은 목적 함수에 제약 조건을 추가하여 새로운 함수를 만들고, 이 새로운 함수를 최대화하거나 최소화하는 변수 값을 찾는 방법이다.
Feasible Region; 가능한 영역
제약 조건을 만족하는 변수들의 영역
목적 함수를 최대화 또는 최소화할 때, 탐색해야 하는 변수들의 범위를 나타낸다. 가능한 영역 내에서 목적 함수의 최적 값을 찾아야 제약 조건을 만족하면서 문제의 해를 구할 수 있다.
예로 선형 제약 조건이 있는 최적화 문제를 생각하면 목적 함수는 Z(x, y) = 3x + 2y이고, 선형 부등식 제약 조건:
x + y ≤ 4
x ≥ 0
y ≥ 0
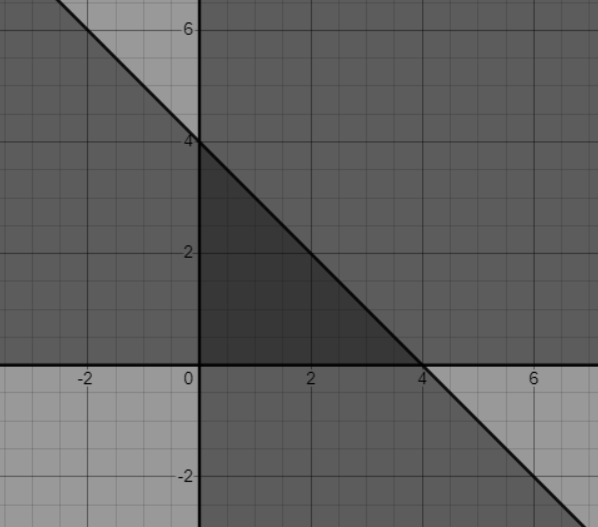
이 경우 가능한 영역은 1번, 2번, 3번 제약 조건을 만족하는 (x, y)의 집합이고 이 영역은 원점, (4,0), (0,4)를 꼭짓점으로 하는 삼각형이 되고. 이 삼각형 내에서 목적 함수 Z(x, y)를 최대화하는 (x, y) 값을 찾아야 한다.
위에서 설명한 라그랑주 승수법 등의 기법을 통해 제약 조건을 만족하는 변수들의 영역을 탐색하여 목적 함수를 최대화하거나 최소화하는 해를 찾아내야 한다.
'Machine Learning' 카테고리의 다른 글
| RV / 이산&연속형 확률변수 합산 방식 차이, 특징, 평균과 분산 (0) | 2023.04.06 |
|---|---|
| Concept/ Random Variables 확률변수 (0) | 2023.04.06 |
| Concept/ Decision Variable 결정변수 (0) | 2023.04.04 |
| Concept/ Objective Functions 목적함수 (단일/다중 목적 문제) (0) | 2023.04.04 |
| Concept/ Bayesian & Frequentist statistical approaches 베이지안&프리퀀티스트 접근 (0) | 2023.04.04 |
목차
개요
unconstrained(비구속 최적화)와 constrained optimization(구속 최적화)
그리고 제약의 분류인 equality(등식 제약)와 inequality constraint(부등식 제약)에 대해 알아보자
Unconstrained Optimization; 제약이 없는 최적화
문제의 해결 방법에서 제약 조건이 없는 최적화를 의미
목적 함수(objective function)를 최대화하거나 최소화하는 변수의 값을 찾는 것이 목표입니다.
예를 들어, 어떤 기업이 이익을 최대화하는 생산량을 찾고자 한다면, 이익 함수를 최대화하는 생산량 값을 찾는 것이 unconstrained optimization 문제가 됩니다.
하지만 대부분의 ML에서는 비구속 최적화를 실행하기 보다는 구속 최적화를 실행하기에 개념 이해만 하면된다.
제약이 없는 최적화는 보통 미분을 사용해 해결할 수 있다. 최대값이건 최소값이건 제한 조건이 없기 때문에 목적 함수를 변수에 대해 미분하여 그 기울기가 0이 되는 점을 찾게 된다면 찾을 수 있다.
constrained optimization; 제약이 있는 최적화
목적 함수를 최대화하거나 최소화하는 동시에 일정한 제약 조건을 만족해야 하는 최적화
제약 조건은 equality constraint(등식 제약)과 inequality constraint(부등식 제약)로 구분할 수 있다.
Equality Constraint (등식 제약)
등식 제약은 최적화 문제에서 변수들 사이에 주어진 관계를 나타내는 등식.
예를 들어, 어떤 기업이 이익을 최대화하는 생산량을 찾고자 하는데, 제품 A와 제품 B의 생산량의 합이 정해져 있다면(=) 이러한 제약 조건은 equality constraint로 볼 수 있다.
Inequality Constraint (부등식 제약)
부등식 제약은 최적화 문제에서 변수들 사이에 주어진 관계를 나타내는 부등식.
예를 들어, 어떤 기업이 이익을 최대화하는 생산량을 찾고자 하는데, 제품 A의 생산량이 제품 B의 생산량보다 크거나 같아야 한다면(>=) 이러한 제약 조건은 inequality constraint로 볼 수 있다.
제약이 있는 최적화에서는 일반적으로 라그랑주 승수법(Lagrange Multipliers) 등의 기법을 사용하여 해결한다.
라그랑주 승수법은 목적 함수에 제약 조건을 추가하여 새로운 함수를 만들고, 이 새로운 함수를 최대화하거나 최소화하는 변수 값을 찾는 방법이다.
Feasible Region; 가능한 영역
제약 조건을 만족하는 변수들의 영역
목적 함수를 최대화 또는 최소화할 때, 탐색해야 하는 변수들의 범위를 나타낸다. 가능한 영역 내에서 목적 함수의 최적 값을 찾아야 제약 조건을 만족하면서 문제의 해를 구할 수 있다.
예로 선형 제약 조건이 있는 최적화 문제를 생각하면 목적 함수는 Z(x, y) = 3x + 2y이고, 선형 부등식 제약 조건:
x + y ≤ 4
x ≥ 0
y ≥ 0

이 경우 가능한 영역은 1번, 2번, 3번 제약 조건을 만족하는 (x, y)의 집합이고 이 영역은 원점, (4,0), (0,4)를 꼭짓점으로 하는 삼각형이 되고. 이 삼각형 내에서 목적 함수 Z(x, y)를 최대화하는 (x, y) 값을 찾아야 한다.
위에서 설명한 라그랑주 승수법 등의 기법을 통해 제약 조건을 만족하는 변수들의 영역을 탐색하여 목적 함수를 최대화하거나 최소화하는 해를 찾아내야 한다.
'Machine Learning' 카테고리의 다른 글
| RV / 이산&연속형 확률변수 합산 방식 차이, 특징, 평균과 분산 (0) | 2023.04.06 |
|---|---|
| Concept/ Random Variables 확률변수 (0) | 2023.04.06 |
| Concept/ Decision Variable 결정변수 (0) | 2023.04.04 |
| Concept/ Objective Functions 목적함수 (단일/다중 목적 문제) (0) | 2023.04.04 |
| Concept/ Bayesian & Frequentist statistical approaches 베이지안&프리퀀티스트 접근 (0) | 2023.04.04 |
