이항 계수 3(#11401)
- Problem
자연수 \(N\)과 정수 \(K\)가 주어졌을 때 이항 계수 (N,K) 를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
- Hint
주어진 1000000007은 크기가 큰 소수이다.
- Solution
큰수의 곱들의 나머지를 구할 때에는 분할 정복을 이용하여 매번 계산시에 나머지를 구한후 나머지로만 남은 연산을 실시하여도 같은 결과가 나온다는 사실은 알고 있어야한다. (나머지 연산 -모듈러 법칙)
ps. 사실 법칙 네이밍은 중요하지 않다 수학적 원리를 이해할수 있기만 하면된다. 하지만 마지막에 사용하는 페르마 소정리의 경우에는 과거에 올림피아드 등을 준비하지 않았더라면 일반적인 사람이 미리 알고 있기 쉽지않다.
n,k= map(int, input().split())
p= 1000000007
def factorial(N):
n=1
for i in range(2,N+1):
n=(n*i)%p
return n
def expdiv(n,e):
if e==0:
return 1
elif e==1:
return n
else:
td=expdiv(n,e//2)
if e%2:
return td*td*n%p
else:
return td*td%p
top = factorial(n)%p
bottom = expdiv(factorial(n-k)*factorial(k)%p,p-2)
print(top*bottom%p)
1. 이항계수의 정의에 대해서 알기
고등학교때의 수업이 기억이 난다면 nCk 등을 통해 알고 있거나 조합론등에서 파스칼의 삼각형 등의 꼴로 알고 있을 수 있고 이 파스칼의 삼각형의 원리를 사용하여 풀 수 있는 알고리즘 문제도 존재한다.
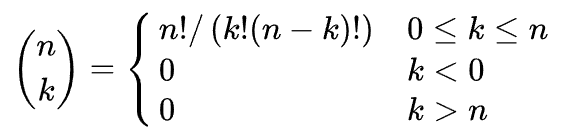
맨 위의 식을 기억하고 있으면 된다.
2. 팩토리오를 계산시에 매번 계산마다 큰 소수인 p로 나머지를 구하여 메모리 오버, 타임오버를 피하기
p= 1000000007
def factorial(N):
n=1
for i in range(2,N+1):
n=(n*i)%p
return n위의 식을 확인하게 된다면 매 계산시마다 p의 나머지를 구하고 있다.
3. 분할 정복을 이용하여 거듭제곱의 값을 구하기
사실 이 문제에 있어서 이항계수의 식을 그대로 풀이에 이용한다면 거듭제곱이 나올 이유가 없지만 이후에 설명할 페르마 소정리 풀이를 위해서 거듭제곱을 효율적으로 구할수 있는 방식이 필요하다. 이는 1629번의 곱셈에서 나온 분할 정복 방식과 비슷한 방식을 사용하면 된다. (하지만 1629번과는 다르게 이 문제에서는 n의 0 승이 존재하는 이유로 조건문으로 0도 처리를 해주어야한다.)
def expdiv(n,e):
if e==0:
return 1
elif e==1:
return n
else:
td=expdiv(n,e//2)
if e%2:
return td*td*n%p
else:
return td*td%p이 또한 거듭제곱의 과정에서 큰 수에 대비하여 p의 나머지로만 계산을 하여야한다.
4 . 페르마의 소정리
백준 내에서 주어지는 문제에 대한 설명을 읽을때 페르마의 소정리를 쓰라고 하면서 곱셈의 역원을 구하는 문제라고 나와있는데 용어가 어렵지
결론부터 설명하자면 위에서 설명하였던 이항 계수 식을 페르마의 소정리로 간단하게 나타낼수 있고 이렇게 나타낸 식이 역원 (항등식의 반대편값 - 컴퓨터연산이 더 효율적인 식)을 이용하면 된다.
먼저 지루하지만 이해에 필요한 정의부터 보자.

합동은 같은 형태, 우리에게는 같은 값을 가져다 준다는 뜻이고 mod 는 깊게 설명하면 어렵지만 mod p 는 양변을 p로 나누고 나머지만 사용한다 이렇게 이해해보자
자 그럼 p가 소수이고 a가 정수일때 a의 p승을 p로 나눈값과 a를 p로 나눈 값이 합동 이라는 말을 이해했을것이다.
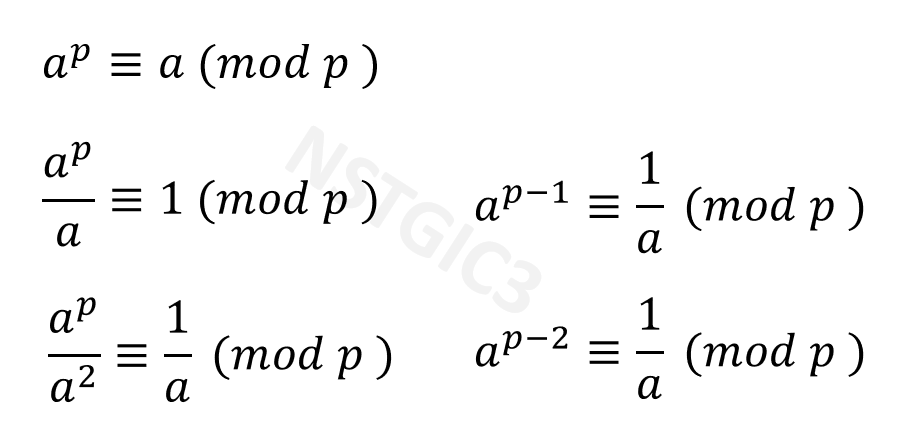
양변에 a를 한번, 두번 나누었을때의 식이다. 이중에 가장 우측 하단의 식에 집중해보자.
먼저 이런 꼴을 만드는 이유에 대해서 생각해보자면 이 문제에서 최종적으로 원하는 식을 분수꼴로 표현을 해주었을때
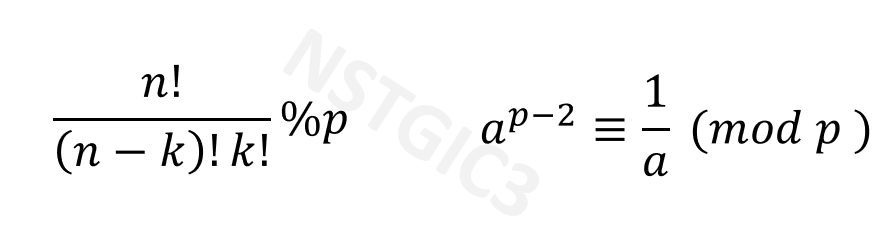
문제풀이를 위한 좌측 식에서 앞의 분수꼴이
1. 정수형태로 나온다는 보장이 없고 2. 값이 메모리 오버를 넘기지 않을 보장도 없다.
그럼 분모에 있는 부분에 대해서 조치를 취해주어야하는데... 바로 그 조치를 페르마의 소정리로 간단하게 표현해줄수 있다.
이부분이 문제의 설명에 있었던 새롭게 표현된 식의 역원을 이용하여 문제를 해결하라는 논점이다.

따라서 위의 사진과 같이 결론적으로는 a가 정수였으니 a 자리에 n-k와 k의 팩토리얼의 곱을 집어넣고 아래 식의 좌측항(곱셈의 역원)을 이용하여 계산을 하면된다.
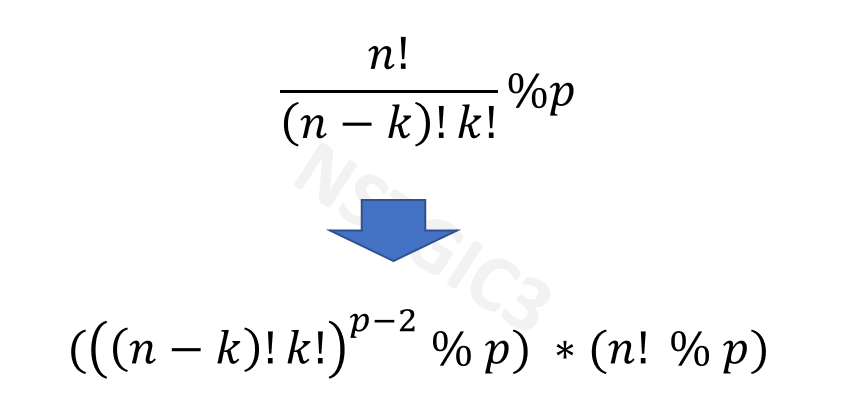
이를 코드로 표현하게된다면
n,k= map(int, input().split())
p= 1000000007
def factorial(N):
n=1
for i in range(2,N+1):
n=(n*i)%p
return n
def expdiv(n,e):
if e==0:
return 1
elif e==1:
return n
else:
td=expdiv(n,e//2)
if e%2:
return td*td*n%p
else:
return td*td%p
top = factorial(n)%p
bottom = expdiv(factorial(n-k)*factorial(k)%p,p-2)
print(top*bottom%p)
'Baekjoon > Indiviual solve' 카테고리의 다른 글
| [백준 1904번] 결과값으로 큰 정수의 나머지를 원하는 경우 (5) | 2022.10.12 |
|---|---|
| [백준 9184번] 깊은 복사,얕은 복사 개념 (0) | 2022.10.12 |
| 백준 2981번[검문] :: 약수 구하기 (0) | 2022.09.02 |
