목차
문제풀이를 하기 전에 이번 단계의 제목인 재귀의 개념에 대해서 간단히 요약하자면
재귀함수란, 어떤 함수에서 자신을 다시 호출하여 작업을 수행하는 방식의 함수를 의미한다.
반복을 하되 문제에서 원한 조건을 만족시키기 위해 함수의 인수 등을 바꾸어 가면서 함수에 적용시켜줘야한다. 따라서 이번 단계에서는 숏코딩 보다는 재귀를 사용하며 문제풀이를 하는 방향으로 풀이를 하겠다
팩토리얼(#10872)
- Problem
0보다 크거나 같은 정수 N이 주어진다. 이때, N!을 출력하는 프로그램을 작성하시오.
- Hint
N!은 N부터 1씩 감소하는 정수를 계속 곱해가는 연산방법이다.
- Solution
재귀을 이용한 풀이
def fac(n):
global res
if n==0:
print(res)
return
else:
res=res*n
fac(n-1)
res =1
fac(int(input()))fac함수를 n이 0이 될때까지 n의 값을 1씩 줄여가면서 계속 호출을 하게 프로그래밍 하였다. result의 초기값을 1로 두어 n을 곱하였을때 n이 출력이 되게 하였다.
피보나치 수 5(#10870)
- Problem
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가 된다. n=17일때 까지 피보나치 수를 써보면 다음과 같다. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.
- Hint
0번째 수와 1번째 수는 특수 케이스라고 생각을 하고 문제를 풀어보자
- Solution
재귀를 이용한 풀이
def fibo(n):
n=int(n)
if n==0:
return 0
elif n==1:
return 1
else:
return fibo(n-1)+fibo(n-2)
print(fibo(input()))0번째 수는 0이고 1번째 수는 1이고 나머지으 경우에는 n-1 번째와 n-2 번째를 호출하여 결과를 나타내게 하였다.
재귀함수가 뭔가요?(#17478)
- Problem
평소에 질문을 잘 받아주기로 유명한 중앙대학교의 JH 교수님은 학생들로부터 재귀함수가 무엇인지에 대하여 많은 질문을 받아왔다. 매번 질문을 잘 받아주셨던 JH 교수님이지만 그는 중앙대학교가 자신과 맞는가에 대한 고민을 항상 해왔다. 중앙대학교와 자신의 길이 맞지 않다고 생각한 JH 교수님은 결국 중앙대학교를 떠나기로 결정하였다. 떠나기 전까지도 제자들을 생각하셨던 JH 교수님은 재귀함수가 무엇인지 물어보는 학생들을 위한 작은 선물로 자동 응답 챗봇을 준비하기로 했다. JH 교수님이 만들 챗봇의 응답을 출력하는 프로그램을 만들어보자.
- Hint
여러 줄의 문장이 있어서 혼란스러울 수 있지만 이를 문자로 치환하여 간단히 생각해보자.
- Solution
재귀를 이용한 풀이
def brokenradio(n):
n=int(n)
a = "____"*(c-n)
if n==0:
print(f'{a}\"재귀함수가 뭔가요?\"\n{a}"재귀함수는 자기 자신을 호출하는 함수라네\"')
print(f"{a}라고 답변하였지.")
return
else:
print(f'{a}\"재귀함수가 뭔가요?\"\n{a}\"잘 들어보게. 옛날옛날 한 산 꼭대기에 이세상 모든 지식을 통달한 선인이 있었어.\n{a}마을 사람들은 모두 그 선인에게 수많은 질문을 했고, 모두 지혜롭게 대답해 주었지.\n{a}그의 답은 대부분 옳았다고 하네. 그런데 어느 날, 그 선인에게 한 선비가 찾아와서 물었어.\"')
n-=1
brokenradio(n)
print(f'{a}라고 답변하였지.')
global c
c = int(input())
print("어느 한 컴퓨터공학과 학생이 유명한 교수님을 찾아가 물었다.")
brokenradio(c)마치 고장난 라디오 같아서 br이라고 함수명을 지어주었다. 마지막의 경우와 나머지의 경우에 출력하는 내용이 다르고 반복이 될 수록 앞에의 ' - ' dash 의 개수가 늘어나는 것을 변수 a 로 할당하여 f-string 을 이용하여 출력해주었다.
별 찍기 - 10(#2447)
- Problem
재귀적인 패턴으로 별을 찍어 보자. N이 3의 거듭제곱(3, 9, 27, ...)이라고 할 때, 크기 N의 패턴은 N×N 정사각형 모양이다. 크기 3의 패턴은 가운데에 공백이 있고, 가운데를 제외한 모든 칸에 별이 하나씩 있는 패턴이다. *** * * *** N이 3보다 클 경우, 크기 N의 패턴은 공백으로 채워진 가운데의 (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태이다. 예를 들어 크기 27의 패턴은 예제 출력 1과 같다.
- Hint
결국에는 출력은 1줄씩 되고 3줄이 한 덩어리로 생각하고 출력을 하려해도 1줄씩 반복하여 출력을 시켜줘야 올바르게 출력이 된다.
- Solution
재귀를 이용한 풀이
def star(n):
if n==3:
f="***"
h="* *"
a=[f,h,f]
return a
else:
ff=[]
for i in star(n//3):
ii=i*3
ff.append(ii)
hh=[]
for i in star(n//3):
ii=i+" "*(n//3)+i
hh.append(ii)
res=[ff,hh,ff]
res=sum(res,[])
return res
print(*star(int(input())),sep='\n')첫번째 출력의 경우인 3*3 모양의 각 줄을 f(fill), h(hole), f 라고 저장을 해주고 단계가 1개씩 늘어 날 때마다 가로로 기존의 패턴이 3번 반복 되는 것을 구현 하기 위해서 ii에 이전의 패턴들을 3번씩 반복하는 것을 할당한 후에 ff 리스트에 추가해주었다. 마찬가지로 가운데에 공백이 있는 경우에는 ii에 이전의 패턴 사이에 n//3 만큼의 공백을 추가 시켜 할당한 후에 hh 리스트에 추가 시켜주었다.
여기서 주의해야할 점은 자신이 저장한 리스트의 형식이 필요한 부분에 줄바꿈이 이루어질 수 있도록 필요한 단위만큼 덩어리로 저장되어 있는지 확인을 해주어야 한다. 또한 각 조건문 별로의 return의 형식도 동일하게 짜주어야한다.
위의 문제풀이 방식을 예로 들면 ff와 hh에 append 를 이용하여 이전 문양을 가지고 줄바꿈을 해주면서 파트를 만들어주었고 if n==3 인 경우(처음의 경우)에서의 return 형식 과 같은 형식으로 [f,h,f]과 [ff,hh,ff] 처럼 출력 형식을 맞춰주었다.
당연한 사실이라고 생각하지만 이런 문제에서의 오답은 대부분 출력 형식이나 줄바꿈 등의 실수에서 일어났다.
하노이 탑 이동 순서(#11729)
- Problem
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다. 이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다. 아래 그림은 원판이 5개인 경우의 예시이다.
- Hint
규칙을 찾기 어려울 때에는 직접 써보면서 규칙을 찾아보자
- Solution
재귀를 이용한 풀이
def top(n):
if n==1:
c=1
return c
else:
c=top(n-1)*2+1
return c
def route(n,a,b,c):
if n==1:
print(a,c)
else:
route(n-1,a,c,b)
print(a,c)
route(n-1,b,a,c)
i = int(input())
print(top(i))
route(i,1,2,3)
top함수로는 최소 이동 횟수를 출력하도록 하였고 이 또한 재귀를 사용하여 예전 값의 2배에 -1 을 해주면 값이 나온다.
이동 경로 같은 경우에는
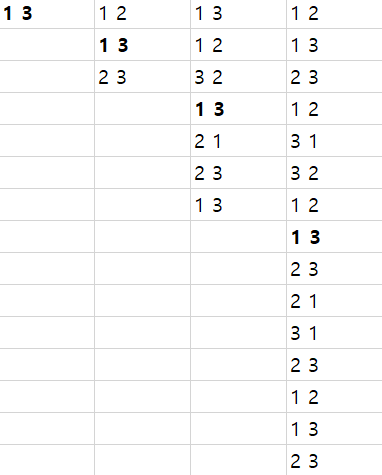
위의 표를 잘 살펴보면 1 3에 하이라이트를 해놓은걸 볼 수 있는데 이 case가 기준이 된다. 이는 최대 사이즈의 원판을 최우측에 놓는 case로 하노이탑의 조건 상 나오지 않을 수 없는 case 이며 이것을 기준으로 n 사이즈의 원판위에 n-1 개의 원판 세트를 옮기는 규칙이 나오게 된다.
많이 생각을 한 사용자라면 n이 홀수 일 때는 1개짜리 원판이 우측에 짝수 일때는 가운데에 놓인다는 사실을 알고 있고 이는 곧 홀수일 때는 3(우측)으로 옮겨지는게 짝수 일때는 2(중앙)으로 놓이지만 항상 1에서 나온다는 사실을 생각 할 수 있다. 이해를 돕기 위해 다시 위의 그림을 보면서 설명을 하자면 1 3 을 기준으로

당연히 1은 그대로 있고 2 3 의 위치만 바뀜을 확인 할 수 있다.
따라서 n개 세트의 1 3 이전의 이동규칙은
n-1 의 이동 규칙이되, n-1의 최대 원판은 n 에서의 최대 원판 이전의 원판이 들어갈 자리 이므로 2와 3의 자리를 스왑 해주어야 한다.
그럼 n의 경우에는 1 3 이후의 이동 규칙은 무엇일까? 위에서 설명을 할때
이것을 기준으로 n 사이즈의 원판위에 n-1 개의 원판 세트를 옮기는 규칙이 나오게 된다.
결국에 n개 세트의 1 3 이후의 이동규칙은
n-1개의 세트에서의 이동 경로와 비슷한 메카니즘이되, n-1 번째의 경우엔 최대 크기의 원판이 n-1 이어서 이를 3에 가져다 준 것만 같고 나머지 1과 2의 위치를 스왑 해주어야 한다.
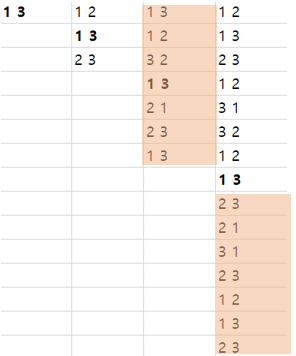
결론적으로 n의 경우에는
n개 세트의 1 3 이전의 이동규칙은
n-1 의 이동 규칙이되, n-1의 최대 원판은 n 에서의 최대 원판 이전의 원판이 들어갈 자리 이므로 2와 3의 자리를 스왑 해주어야 한다.
1 3 을 출력해준다.
n개 세트의 1 3 이후의 이동규칙은
n-1개의 세트에서의 이동 경로와 비슷한 메카니즘이되, n-1 번째의 경우엔 최대 크기의 원판이 n-1 이어서 이를 3에 가져다 준 것만 같고 나머지 1과 2의 위치를 스왑 해주어야 한다.
로 생각을 할 수 있고 이를 프로그래밍으로 나타내게 되면
def route(n,a,b,):
if n==1:
print(a,c)
else:
route(n-1,a,c,b)
print(a,c)
route(n-1,b,a,c)route(i,1,2,3) 로 실행
이 되게 된것이다.
'Baekjoon > Stepbystep' 카테고리의 다른 글
| [백준/python] 정렬 전체 풀이(11단계) (0) | 2022.08.27 |
|---|---|
| [백준/python] 브루트 포스 전체 풀이(10단계) (0) | 2022.08.08 |
| [백준/python] 기본 수학 2 전체 풀이(8단계) (0) | 2022.08.02 |
| [백준/python] 기본 수학 1 전체 풀이(7단계) (0) | 2022.08.01 |
| [백준/python] 문자열 전체 풀이(6단계) (0) | 2022.07.31 |
목차
문제풀이를 하기 전에 이번 단계의 제목인 재귀의 개념에 대해서 간단히 요약하자면
재귀함수란, 어떤 함수에서 자신을 다시 호출하여 작업을 수행하는 방식의 함수를 의미한다.
반복을 하되 문제에서 원한 조건을 만족시키기 위해 함수의 인수 등을 바꾸어 가면서 함수에 적용시켜줘야한다. 따라서 이번 단계에서는 숏코딩 보다는 재귀를 사용하며 문제풀이를 하는 방향으로 풀이를 하겠다
팩토리얼(#10872)
- Problem
0보다 크거나 같은 정수 N이 주어진다. 이때, N!을 출력하는 프로그램을 작성하시오.
- Hint
N!은 N부터 1씩 감소하는 정수를 계속 곱해가는 연산방법이다.
- Solution
재귀을 이용한 풀이
def fac(n):
global res
if n==0:
print(res)
return
else:
res=res*n
fac(n-1)
res =1
fac(int(input()))fac함수를 n이 0이 될때까지 n의 값을 1씩 줄여가면서 계속 호출을 하게 프로그래밍 하였다. result의 초기값을 1로 두어 n을 곱하였을때 n이 출력이 되게 하였다.
피보나치 수 5(#10870)
- Problem
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가 된다. n=17일때 까지 피보나치 수를 써보면 다음과 같다. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.
- Hint
0번째 수와 1번째 수는 특수 케이스라고 생각을 하고 문제를 풀어보자
- Solution
재귀를 이용한 풀이
def fibo(n):
n=int(n)
if n==0:
return 0
elif n==1:
return 1
else:
return fibo(n-1)+fibo(n-2)
print(fibo(input()))0번째 수는 0이고 1번째 수는 1이고 나머지으 경우에는 n-1 번째와 n-2 번째를 호출하여 결과를 나타내게 하였다.
재귀함수가 뭔가요?(#17478)
- Problem
평소에 질문을 잘 받아주기로 유명한 중앙대학교의 JH 교수님은 학생들로부터 재귀함수가 무엇인지에 대하여 많은 질문을 받아왔다. 매번 질문을 잘 받아주셨던 JH 교수님이지만 그는 중앙대학교가 자신과 맞는가에 대한 고민을 항상 해왔다. 중앙대학교와 자신의 길이 맞지 않다고 생각한 JH 교수님은 결국 중앙대학교를 떠나기로 결정하였다. 떠나기 전까지도 제자들을 생각하셨던 JH 교수님은 재귀함수가 무엇인지 물어보는 학생들을 위한 작은 선물로 자동 응답 챗봇을 준비하기로 했다. JH 교수님이 만들 챗봇의 응답을 출력하는 프로그램을 만들어보자.
- Hint
여러 줄의 문장이 있어서 혼란스러울 수 있지만 이를 문자로 치환하여 간단히 생각해보자.
- Solution
재귀를 이용한 풀이
def brokenradio(n):
n=int(n)
a = "____"*(c-n)
if n==0:
print(f'{a}\"재귀함수가 뭔가요?\"\n{a}"재귀함수는 자기 자신을 호출하는 함수라네\"')
print(f"{a}라고 답변하였지.")
return
else:
print(f'{a}\"재귀함수가 뭔가요?\"\n{a}\"잘 들어보게. 옛날옛날 한 산 꼭대기에 이세상 모든 지식을 통달한 선인이 있었어.\n{a}마을 사람들은 모두 그 선인에게 수많은 질문을 했고, 모두 지혜롭게 대답해 주었지.\n{a}그의 답은 대부분 옳았다고 하네. 그런데 어느 날, 그 선인에게 한 선비가 찾아와서 물었어.\"')
n-=1
brokenradio(n)
print(f'{a}라고 답변하였지.')
global c
c = int(input())
print("어느 한 컴퓨터공학과 학생이 유명한 교수님을 찾아가 물었다.")
brokenradio(c)마치 고장난 라디오 같아서 br이라고 함수명을 지어주었다. 마지막의 경우와 나머지의 경우에 출력하는 내용이 다르고 반복이 될 수록 앞에의 ' - ' dash 의 개수가 늘어나는 것을 변수 a 로 할당하여 f-string 을 이용하여 출력해주었다.
별 찍기 - 10(#2447)
- Problem
재귀적인 패턴으로 별을 찍어 보자. N이 3의 거듭제곱(3, 9, 27, ...)이라고 할 때, 크기 N의 패턴은 N×N 정사각형 모양이다. 크기 3의 패턴은 가운데에 공백이 있고, 가운데를 제외한 모든 칸에 별이 하나씩 있는 패턴이다. *** * * *** N이 3보다 클 경우, 크기 N의 패턴은 공백으로 채워진 가운데의 (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태이다. 예를 들어 크기 27의 패턴은 예제 출력 1과 같다.
- Hint
결국에는 출력은 1줄씩 되고 3줄이 한 덩어리로 생각하고 출력을 하려해도 1줄씩 반복하여 출력을 시켜줘야 올바르게 출력이 된다.
- Solution
재귀를 이용한 풀이
def star(n):
if n==3:
f="***"
h="* *"
a=[f,h,f]
return a
else:
ff=[]
for i in star(n//3):
ii=i*3
ff.append(ii)
hh=[]
for i in star(n//3):
ii=i+" "*(n//3)+i
hh.append(ii)
res=[ff,hh,ff]
res=sum(res,[])
return res
print(*star(int(input())),sep='\n')첫번째 출력의 경우인 3*3 모양의 각 줄을 f(fill), h(hole), f 라고 저장을 해주고 단계가 1개씩 늘어 날 때마다 가로로 기존의 패턴이 3번 반복 되는 것을 구현 하기 위해서 ii에 이전의 패턴들을 3번씩 반복하는 것을 할당한 후에 ff 리스트에 추가해주었다. 마찬가지로 가운데에 공백이 있는 경우에는 ii에 이전의 패턴 사이에 n//3 만큼의 공백을 추가 시켜 할당한 후에 hh 리스트에 추가 시켜주었다.
여기서 주의해야할 점은 자신이 저장한 리스트의 형식이 필요한 부분에 줄바꿈이 이루어질 수 있도록 필요한 단위만큼 덩어리로 저장되어 있는지 확인을 해주어야 한다. 또한 각 조건문 별로의 return의 형식도 동일하게 짜주어야한다.
위의 문제풀이 방식을 예로 들면 ff와 hh에 append 를 이용하여 이전 문양을 가지고 줄바꿈을 해주면서 파트를 만들어주었고 if n==3 인 경우(처음의 경우)에서의 return 형식 과 같은 형식으로 [f,h,f]과 [ff,hh,ff] 처럼 출력 형식을 맞춰주었다.
당연한 사실이라고 생각하지만 이런 문제에서의 오답은 대부분 출력 형식이나 줄바꿈 등의 실수에서 일어났다.
하노이 탑 이동 순서(#11729)
- Problem
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다. 이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다. 아래 그림은 원판이 5개인 경우의 예시이다.
- Hint
규칙을 찾기 어려울 때에는 직접 써보면서 규칙을 찾아보자
- Solution
재귀를 이용한 풀이
def top(n):
if n==1:
c=1
return c
else:
c=top(n-1)*2+1
return c
def route(n,a,b,c):
if n==1:
print(a,c)
else:
route(n-1,a,c,b)
print(a,c)
route(n-1,b,a,c)
i = int(input())
print(top(i))
route(i,1,2,3)
top함수로는 최소 이동 횟수를 출력하도록 하였고 이 또한 재귀를 사용하여 예전 값의 2배에 -1 을 해주면 값이 나온다.
이동 경로 같은 경우에는

위의 표를 잘 살펴보면 1 3에 하이라이트를 해놓은걸 볼 수 있는데 이 case가 기준이 된다. 이는 최대 사이즈의 원판을 최우측에 놓는 case로 하노이탑의 조건 상 나오지 않을 수 없는 case 이며 이것을 기준으로 n 사이즈의 원판위에 n-1 개의 원판 세트를 옮기는 규칙이 나오게 된다.
많이 생각을 한 사용자라면 n이 홀수 일 때는 1개짜리 원판이 우측에 짝수 일때는 가운데에 놓인다는 사실을 알고 있고 이는 곧 홀수일 때는 3(우측)으로 옮겨지는게 짝수 일때는 2(중앙)으로 놓이지만 항상 1에서 나온다는 사실을 생각 할 수 있다. 이해를 돕기 위해 다시 위의 그림을 보면서 설명을 하자면 1 3 을 기준으로

당연히 1은 그대로 있고 2 3 의 위치만 바뀜을 확인 할 수 있다.
따라서 n개 세트의 1 3 이전의 이동규칙은
n-1 의 이동 규칙이되, n-1의 최대 원판은 n 에서의 최대 원판 이전의 원판이 들어갈 자리 이므로 2와 3의 자리를 스왑 해주어야 한다.
그럼 n의 경우에는 1 3 이후의 이동 규칙은 무엇일까? 위에서 설명을 할때
이것을 기준으로 n 사이즈의 원판위에 n-1 개의 원판 세트를 옮기는 규칙이 나오게 된다.
결국에 n개 세트의 1 3 이후의 이동규칙은
n-1개의 세트에서의 이동 경로와 비슷한 메카니즘이되, n-1 번째의 경우엔 최대 크기의 원판이 n-1 이어서 이를 3에 가져다 준 것만 같고 나머지 1과 2의 위치를 스왑 해주어야 한다.

결론적으로 n의 경우에는
n개 세트의 1 3 이전의 이동규칙은
n-1 의 이동 규칙이되, n-1의 최대 원판은 n 에서의 최대 원판 이전의 원판이 들어갈 자리 이므로 2와 3의 자리를 스왑 해주어야 한다.
1 3 을 출력해준다.
n개 세트의 1 3 이후의 이동규칙은
n-1개의 세트에서의 이동 경로와 비슷한 메카니즘이되, n-1 번째의 경우엔 최대 크기의 원판이 n-1 이어서 이를 3에 가져다 준 것만 같고 나머지 1과 2의 위치를 스왑 해주어야 한다.
로 생각을 할 수 있고 이를 프로그래밍으로 나타내게 되면
def route(n,a,b,):
if n==1:
print(a,c)
else:
route(n-1,a,c,b)
print(a,c)
route(n-1,b,a,c)route(i,1,2,3) 로 실행
이 되게 된것이다.
'Baekjoon > Stepbystep' 카테고리의 다른 글
| [백준/python] 정렬 전체 풀이(11단계) (0) | 2022.08.27 |
|---|---|
| [백준/python] 브루트 포스 전체 풀이(10단계) (0) | 2022.08.08 |
| [백준/python] 기본 수학 2 전체 풀이(8단계) (0) | 2022.08.02 |
| [백준/python] 기본 수학 1 전체 풀이(7단계) (0) | 2022.08.01 |
| [백준/python] 문자열 전체 풀이(6단계) (0) | 2022.07.31 |
