목차
개요
이번 포스트에서는 표준 정규 분포(Standard Normal Distribution)와 Z-점수(Z-score)에 대해서 알아본다.
또한 표준정규분포를 따르는 데이터들(표준화된) 확률변수인 표준확률변수(standard random variable)에 대해서 알아본다.
정의와 실제 통계학에서 어떻게 쓰이는지에 대해서 알아본다.
정의
표준 정규 분포(Standard Normal Distribution)
표준 정규 분포는 통계학에서 가장 잘 알려진 확률 분포 중 하나인데 그 이유로는 이름에서도 알 수 있다싶이 스탠다드한 표준 형태이기 때문이다. 그만큼 우리 주변에서 가장 많이 볼 수있는데 예로들어 수능이나 시험을 보고 9등급으로의 계열을 나눌때도 이 분포를 사용하고 표준편차라고 불리우는 편차 또한 이 분포형태에서의 표준 편차를 의미하는 것이다.
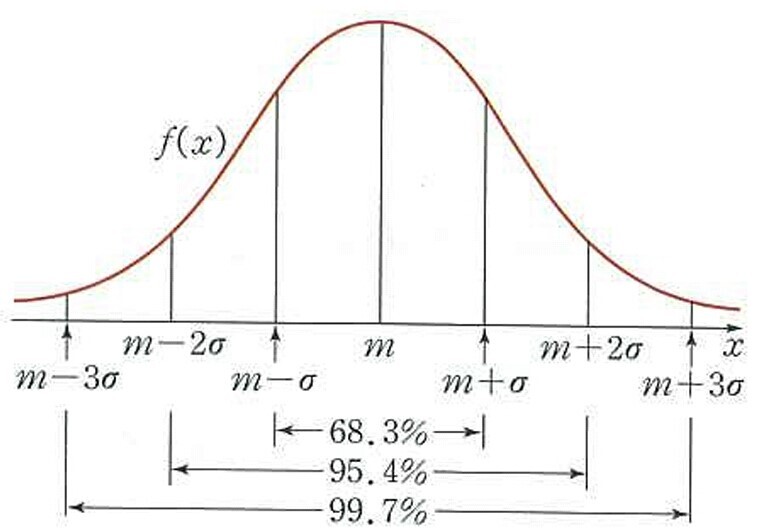
정의를 보자면 평균이 0이고 표준편차가 1인 정규 분포를 뜻하는데 종 모양의 그래프로 나타나며, 양 끝으로 갈수록 확률이 낮아지는 특징이 있다.
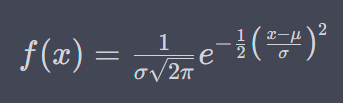
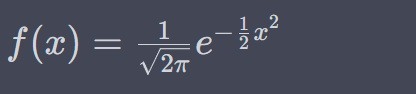
Z-점수(Z-Score)
Z-점수는 원래 데이터를 표준화하여 표준 정규 분포와 비교한 값이고 이것을 표준확률변수(standard random variable)라고 말한다.
각 데이터 포인트의 Z-점수는 해당 포인트가 평균에서 얼마나 떨어져 있는지를 표준 편차 단위로 나타낸다.
Z-점수 = (데이터 포인트 - 평균) / 표준편차
Z = (X - μ) / σ
나중에 이 Z-Score은 표준 정규 분포로의 표준화(standardization)를 위한 정규 분포를 따르는 확률 변수를 표준화하기 위해 사용되는 Z-분포(Z-distribution)의 사용에 있어서 확률을 계산하는데 사용이 된다.
이처럼 표준 정규 분포가 가지는 특성이 복잡한 계산이나 수식을 거치지 않고 도출해낼수 있는 유의미한 값들이 있기 때문에 표준화를 실시하기도 한다.
Z-분포에 대해서 조금 더 말하자면 표준화된 값이 정규 분포내에 어디에 위치해 있는지 정의해주는 분포이기 때문에 Z-점수를 표준화 하였을시 이를 이용해서 확률을 계산할 수 있다.
마무리
표준 정규 분포와 Z-점수를 활용하면 다양한 분야에서 데이터를 비교, 분석하고, 이상치를 찾거나 예측 모델을 만드는 데 도움이 되고 신뢰구간, 가설 검정 등 고급 통계 기법의 기초가 되는 개념(머신러닝에 필요한 부분이다!) 이기에 다양한 데이터를 분석하고 결과를 도출 할때에 유용하게 쓰인다.
'Machine Learning' 카테고리의 다른 글
| RV / Probability Density&Cumulative Distribution Function 확률밀도&누적분포 함수 (0) | 2023.04.08 |
|---|---|
| RV / moment 모멘트; 확률 분포의 특성 (0) | 2023.04.06 |
| RV / non-linear & linear TF 확률 변수 비선형 & 선형 변환 (0) | 2023.04.06 |
| RV / 이산&연속형 확률변수 합산 방식 차이, 특징, 평균과 분산 (0) | 2023.04.06 |
| Concept/ Random Variables 확률변수 (0) | 2023.04.06 |
목차
개요
이번 포스트에서는 표준 정규 분포(Standard Normal Distribution)와 Z-점수(Z-score)에 대해서 알아본다.
또한 표준정규분포를 따르는 데이터들(표준화된) 확률변수인 표준확률변수(standard random variable)에 대해서 알아본다.
정의와 실제 통계학에서 어떻게 쓰이는지에 대해서 알아본다.
정의
표준 정규 분포(Standard Normal Distribution)
표준 정규 분포는 통계학에서 가장 잘 알려진 확률 분포 중 하나인데 그 이유로는 이름에서도 알 수 있다싶이 스탠다드한 표준 형태이기 때문이다. 그만큼 우리 주변에서 가장 많이 볼 수있는데 예로들어 수능이나 시험을 보고 9등급으로의 계열을 나눌때도 이 분포를 사용하고 표준편차라고 불리우는 편차 또한 이 분포형태에서의 표준 편차를 의미하는 것이다.

정의를 보자면 평균이 0이고 표준편차가 1인 정규 분포를 뜻하는데 종 모양의 그래프로 나타나며, 양 끝으로 갈수록 확률이 낮아지는 특징이 있다.
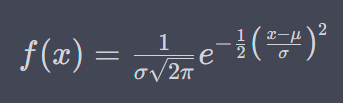
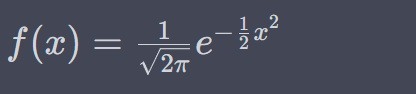
Z-점수(Z-Score)
Z-점수는 원래 데이터를 표준화하여 표준 정규 분포와 비교한 값이고 이것을 표준확률변수(standard random variable)라고 말한다.
각 데이터 포인트의 Z-점수는 해당 포인트가 평균에서 얼마나 떨어져 있는지를 표준 편차 단위로 나타낸다.
Z-점수 = (데이터 포인트 - 평균) / 표준편차
Z = (X - μ) / σ
나중에 이 Z-Score은 표준 정규 분포로의 표준화(standardization)를 위한 정규 분포를 따르는 확률 변수를 표준화하기 위해 사용되는 Z-분포(Z-distribution)의 사용에 있어서 확률을 계산하는데 사용이 된다.
이처럼 표준 정규 분포가 가지는 특성이 복잡한 계산이나 수식을 거치지 않고 도출해낼수 있는 유의미한 값들이 있기 때문에 표준화를 실시하기도 한다.
Z-분포에 대해서 조금 더 말하자면 표준화된 값이 정규 분포내에 어디에 위치해 있는지 정의해주는 분포이기 때문에 Z-점수를 표준화 하였을시 이를 이용해서 확률을 계산할 수 있다.
마무리
표준 정규 분포와 Z-점수를 활용하면 다양한 분야에서 데이터를 비교, 분석하고, 이상치를 찾거나 예측 모델을 만드는 데 도움이 되고 신뢰구간, 가설 검정 등 고급 통계 기법의 기초가 되는 개념(머신러닝에 필요한 부분이다!) 이기에 다양한 데이터를 분석하고 결과를 도출 할때에 유용하게 쓰인다.
'Machine Learning' 카테고리의 다른 글
| RV / Probability Density&Cumulative Distribution Function 확률밀도&누적분포 함수 (0) | 2023.04.08 |
|---|---|
| RV / moment 모멘트; 확률 분포의 특성 (0) | 2023.04.06 |
| RV / non-linear & linear TF 확률 변수 비선형 & 선형 변환 (0) | 2023.04.06 |
| RV / 이산&연속형 확률변수 합산 방식 차이, 특징, 평균과 분산 (0) | 2023.04.06 |
| Concept/ Random Variables 확률변수 (0) | 2023.04.06 |
