목차
개요
본 포스팅은 하단의 글을 통해 개념을 숙지하고 와야지 쉽게 이해가 가능하다.
Concept/ Random Variables 확률변수
목차 개요 이번 포스트에서는 확률이론의 기본 개념인 확률 변수에 대해 알아보고 확률 변수의 개념과 종류에 대해 알아본다. Random Variables; 확률 변수 확률 변수는 어떤 사건이 발생할 확률을
nstgic3.tistory.com
이번 포스트에서는 확률 분포의 특성을 나타내는 모멘트(moment)에 대해서 알아본다.
정의
모멘트(moment)는 확률 분포의 특성을 나타내는 값으로, 확률 변수의 함수로 정의된다.
모멘트에 대한 표현식 : n차 모멘트 = E(X^n)
여기서 X는 확률 변수이며, E는 기댓값(expected value)을 나타내는데 따라서 n차 모멘트는 X^n을 확률 분포에 따라 가중 평균한 값이 된다.
모멘트의 종류
1차 모멘트: 평균(mean) : E(X) = μ
2차 모멘트: 분산(variance) : Var(X) = E[(X - μ)^2]
아래에는 1,2차 모멘트에 관련된 유도나 해석 등이 나와있다.
RV / 이산&연속형 확률변수 합산 방식 차이, 특징, 평균과 분산
목차 개요 본 포스팅은 하단의 글을 통해 개념을 숙지하고 와야지 쉽게 이해가 가능하다. Concept/ Random Variables 확률변수 목차 개요 이번 포스트에서는 확률이론의 기본 개념인 확률 변수에 대해
nstgic3.tistory.com
3차 모멘트: 왜도(skewness) : Skew(X) = E[(X - μ)^3] / σ^3
여기서 μ은 X의 평균값이고, σ는 X의 표준편차다.
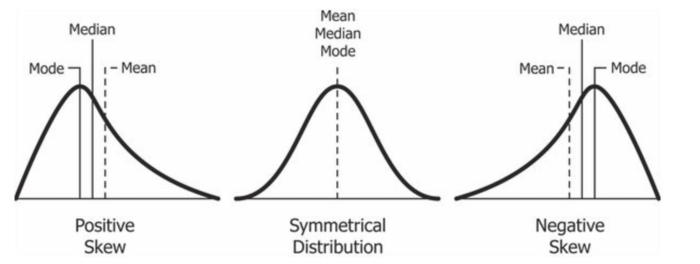
왜도는 데이터가 얼마나 한쪽 방향으로 치우쳐져 있는지를 나타내는 값이라고 생각하면 쉽다.
분포가 완전히 대칭인 경우 왜도는 0이고 데이터의 중심이 평균과 일치하며 이를 정규 분포라고 한다.
(Positive Skewness)
왼쪽 꼬리가 길어지며, 평균이 중앙값보다 큰 값을 가지게 되어 오른쪽으로 치우쳐져 있을 때 왜도는 양수
(Negative Skewness)
오른쪽 꼬리가 길어지며, 평균이 중앙값보다 작은 값을 가지게 되어 왼쪽으로 치우쳐져 있을 때 왜도는 음수
4차 모멘트: 첨도(kurtosis) : Kurt(X) = E[(X - μ)^4] / σ^4 - 3
여기서 μ은 X의 평균값이고, σ는 X의 표준편차다.
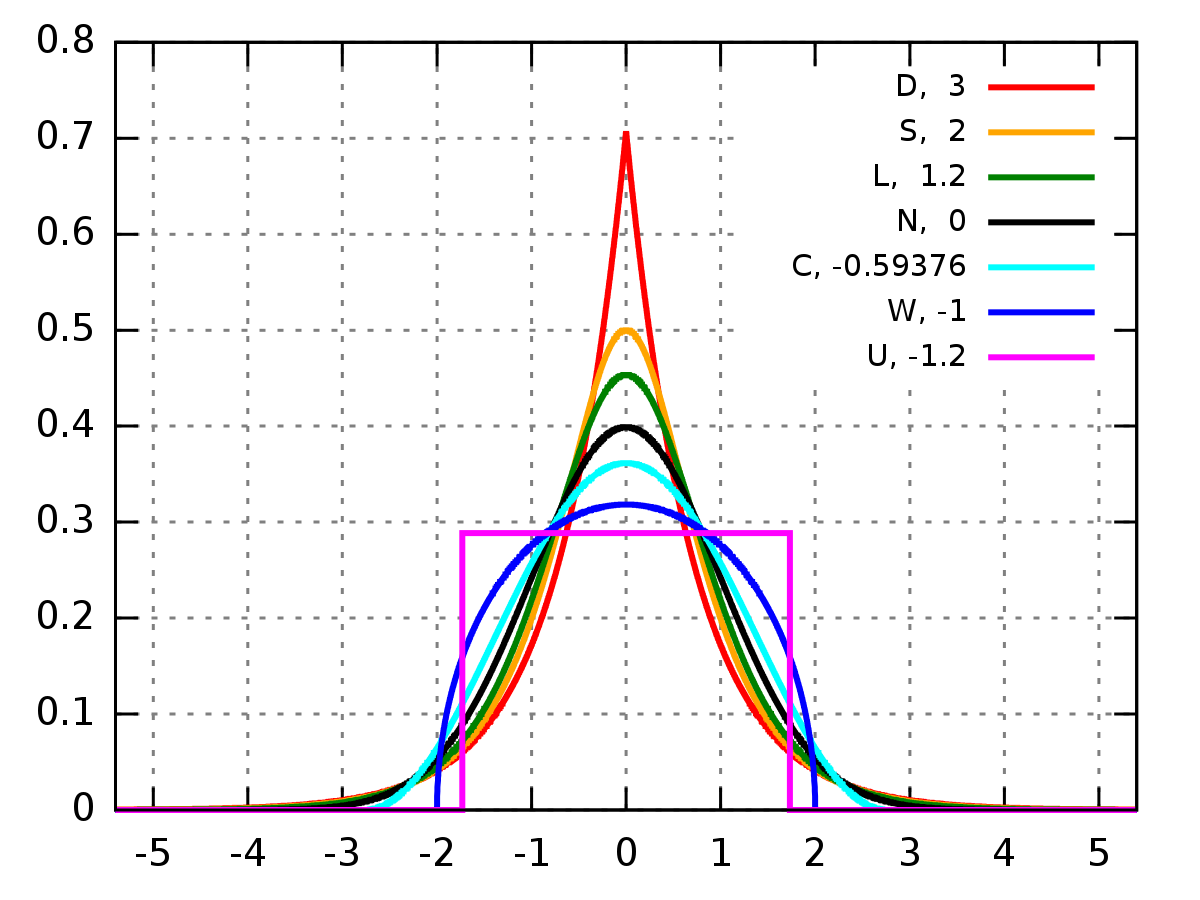
첨도는 분포의 꼬리 부분이 얼마나 뾰족한지를 나타내는 값이라고 생각하면 쉽다.
정규분포의 경우가 바로 첨도가 0인 경우가 되게 되는데 이를 메스커토시스 라고 한다.
레프토커토시스(Leptokurtic)
분포가 뾰족하고 꼬리가 두터운 경우 첨도는 양수이다. 중심 부분의 데이터가 더 집중되어 있으며, 꼬리 부분에 이상치가 더 자주 발생할 가능성이 있다.
플래티커토시스(Platykurtic)
분포가 납작하고 꼬리가 얇은 경우 첨도는 음수이다. 중심 부분의 데이터가 덜 집중되어 있으며, 꼬리 부분에 이상치가 덜 발생할 가능성이 있다.
정규 분포와 같은 대칭적인 분포에서는 첨도가 3에 가깝고 3을 기준으로 3보다 크면 뾰족한 꼬리를 가진 분포를 나타내고, 첨도가 3보다 작으면 완만한 꼬리를 가진 분포를 나타낸다.
마무리
모멘트는 확률 분포의 특성중 비대칭적인 분포에서 중요한 역할을 하며, 이들 값이 큰 경우에는 데이터가 비대칭적으로 분포되어 있음을 나타낸다. 외울 필요는 없고 분산 이후에 왜도와 첨도로 이렇게 나뉘어 놓았다 라고만 인지하면 될것 같다.
'Machine Learning' 카테고리의 다른 글
| Optimaization/Pareto Op 파레토 최적화, 프론티어 (0) | 2023.04.09 |
|---|---|
| RV / Probability Density&Cumulative Distribution Function 확률밀도&누적분포 함수 (0) | 2023.04.08 |
| RV / standard random variable[Z-score] 표준 확률 변수 (0) | 2023.04.06 |
| RV / non-linear & linear TF 확률 변수 비선형 & 선형 변환 (0) | 2023.04.06 |
| RV / 이산&연속형 확률변수 합산 방식 차이, 특징, 평균과 분산 (0) | 2023.04.06 |
목차
개요
본 포스팅은 하단의 글을 통해 개념을 숙지하고 와야지 쉽게 이해가 가능하다.
Concept/ Random Variables 확률변수
목차 개요 이번 포스트에서는 확률이론의 기본 개념인 확률 변수에 대해 알아보고 확률 변수의 개념과 종류에 대해 알아본다. Random Variables; 확률 변수 확률 변수는 어떤 사건이 발생할 확률을
nstgic3.tistory.com
이번 포스트에서는 확률 분포의 특성을 나타내는 모멘트(moment)에 대해서 알아본다.
정의
모멘트(moment)는 확률 분포의 특성을 나타내는 값으로, 확률 변수의 함수로 정의된다.
모멘트에 대한 표현식 : n차 모멘트 = E(X^n)
여기서 X는 확률 변수이며, E는 기댓값(expected value)을 나타내는데 따라서 n차 모멘트는 X^n을 확률 분포에 따라 가중 평균한 값이 된다.
모멘트의 종류
1차 모멘트: 평균(mean) : E(X) = μ
2차 모멘트: 분산(variance) : Var(X) = E[(X - μ)^2]
아래에는 1,2차 모멘트에 관련된 유도나 해석 등이 나와있다.
RV / 이산&연속형 확률변수 합산 방식 차이, 특징, 평균과 분산
목차 개요 본 포스팅은 하단의 글을 통해 개념을 숙지하고 와야지 쉽게 이해가 가능하다. Concept/ Random Variables 확률변수 목차 개요 이번 포스트에서는 확률이론의 기본 개념인 확률 변수에 대해
nstgic3.tistory.com
3차 모멘트: 왜도(skewness) : Skew(X) = E[(X - μ)^3] / σ^3
여기서 μ은 X의 평균값이고, σ는 X의 표준편차다.
왜도는 데이터가 얼마나 한쪽 방향으로 치우쳐져 있는지를 나타내는 값이라고 생각하면 쉽다.
분포가 완전히 대칭인 경우 왜도는 0이고 데이터의 중심이 평균과 일치하며 이를 정규 분포라고 한다.
(Positive Skewness)
왼쪽 꼬리가 길어지며, 평균이 중앙값보다 큰 값을 가지게 되어 오른쪽으로 치우쳐져 있을 때 왜도는 양수
(Negative Skewness)
오른쪽 꼬리가 길어지며, 평균이 중앙값보다 작은 값을 가지게 되어 왼쪽으로 치우쳐져 있을 때 왜도는 음수

4차 모멘트: 첨도(kurtosis) : Kurt(X) = E[(X - μ)^4] / σ^4 - 3
여기서 μ은 X의 평균값이고, σ는 X의 표준편차다.
첨도는 분포의 꼬리 부분이 얼마나 뾰족한지를 나타내는 값이라고 생각하면 쉽다.
정규분포의 경우가 바로 첨도가 0인 경우가 되게 되는데 이를 메스커토시스 라고 한다.
레프토커토시스(Leptokurtic)
분포가 뾰족하고 꼬리가 두터운 경우 첨도는 양수이다. 중심 부분의 데이터가 더 집중되어 있으며, 꼬리 부분에 이상치가 더 자주 발생할 가능성이 있다.
플래티커토시스(Platykurtic)
분포가 납작하고 꼬리가 얇은 경우 첨도는 음수이다. 중심 부분의 데이터가 덜 집중되어 있으며, 꼬리 부분에 이상치가 덜 발생할 가능성이 있다.
정규 분포와 같은 대칭적인 분포에서는 첨도가 3에 가깝고 3을 기준으로 3보다 크면 뾰족한 꼬리를 가진 분포를 나타내고, 첨도가 3보다 작으면 완만한 꼬리를 가진 분포를 나타낸다.

마무리
모멘트는 확률 분포의 특성중 비대칭적인 분포에서 중요한 역할을 하며, 이들 값이 큰 경우에는 데이터가 비대칭적으로 분포되어 있음을 나타낸다. 외울 필요는 없고 분산 이후에 왜도와 첨도로 이렇게 나뉘어 놓았다 라고만 인지하면 될것 같다.
'Machine Learning' 카테고리의 다른 글
| Optimaization/Pareto Op 파레토 최적화, 프론티어 (0) | 2023.04.09 |
|---|---|
| RV / Probability Density&Cumulative Distribution Function 확률밀도&누적분포 함수 (0) | 2023.04.08 |
| RV / standard random variable[Z-score] 표준 확률 변수 (0) | 2023.04.06 |
| RV / non-linear & linear TF 확률 변수 비선형 & 선형 변환 (0) | 2023.04.06 |
| RV / 이산&연속형 확률변수 합산 방식 차이, 특징, 평균과 분산 (0) | 2023.04.06 |
