목차
개요
이번 포스트에서는 확률분포와 관련된 중요한 개념인 확률밀도함수(PDF)와 누적분포함수(CDF)에 대해서 알아본다.
이 포스트에서는 PDF와 CDF의 개념과 차이점을 상세하게 설명하고, 각각의 특징과 활용 방법을 알아보겠습니다.
PDF , CDF 의 정의
확률 밀도함수에 대한 정의를 먼저 이해한 후에 확률 분포함수(누적 분포함수)를 이해하는 것이 더 쉽게 이해가 된다.
확률밀도함수(PDF)
확률밀도함수(Probability Density Function, PDF)는 연속 확률변수의 분포를 설명하는 함수로, 특정 구간에서 확률변수의 값이 나타날 확률을 나타낸다. PDF는 확률변수가 특정 값을 가질 확률 자체를 나타내지 않고, 그 값 근처의 확률을 표현한다.
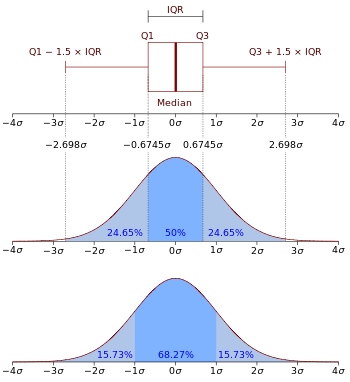
f(x) = dF(x) / dx 꼴로 어렵게 생각하지말고 해당 x 의 f(x)는 그 값의 확률을 나타낸다고 생각하자 값은 항상 0 이상이다.
누적분포함수(CDF)
누적분포함수(Cumulative Distribution Function, CDF)는 확률변수 X가 특정 값 x 이하가 될 확률을 나타낸다.
명칭 그대로 "누적" 하여 확률을 나타내는 식이다. 확률 분포함수라고도 한다.
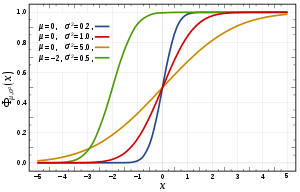
F(x) = P(X ≤ x) 형태로 나타낸다. 당연하게도 x 값은 그 이전값들의 누적값이라서 그렇다. 그래프의 특징으로는 기울기가 음수인 구간이 없다. 즉 x 값이 증가할수록 CDF의 값은 증가하거나 동일하다. 따라서 값 또한 0에서 1 사이에 존재한다.
특징 및 통계학에서의 활용
확률밀도함수(PDF)
1. 기대값 및 분산 계산
평균값 값의 분포 정도를 확인 할 수 있다.
2. 분포의 모양 파악
데이터의 중심 경향성, 퍼짐 정도, 왜곡 등을 파악할 수 있다.
3. 확률밀도의 비교
두 개 이상의 확률분포를 비교할 때 데이터가 어떤 분포에 가까운지, 또는 어떤 변수 간의 관계가 있는지를 분석할 수 있다.
누적분포함수(CDF)
1. 특정 확률 찾기
확률변수가 특정 값 이하가 될 확률을 찾을 수 있다.
2. 신뢰구간 추정
확률변수의 신뢰구간을 추정할 수 있다. 예를 들어, 표본 평균의 95% 신뢰구간을 구하려면, CDF를 사용하여 하위 2.5%와 상위 2.5%의 값을 찾을 수 있다.
마무리
결론적으로는 누적분포함수(CDF)와 확률밀도함수(PDF)의 차이점에 따른 특징을 잘 캐치해서 확률분포를 이해하고 분석하는 데에 적절한 방식을 사용하자
'Machine Learning' 카테고리의 다른 글
| Optimaization/ Lagrange multiplier 라그랑지안 승수법 (0) | 2023.04.09 |
|---|---|
| Optimaization/Pareto Op 파레토 최적화, 프론티어 (0) | 2023.04.09 |
| RV / moment 모멘트; 확률 분포의 특성 (0) | 2023.04.06 |
| RV / standard random variable[Z-score] 표준 확률 변수 (0) | 2023.04.06 |
| RV / non-linear & linear TF 확률 변수 비선형 & 선형 변환 (0) | 2023.04.06 |
목차
개요
이번 포스트에서는 확률분포와 관련된 중요한 개념인 확률밀도함수(PDF)와 누적분포함수(CDF)에 대해서 알아본다.
이 포스트에서는 PDF와 CDF의 개념과 차이점을 상세하게 설명하고, 각각의 특징과 활용 방법을 알아보겠습니다.
PDF , CDF 의 정의
확률 밀도함수에 대한 정의를 먼저 이해한 후에 확률 분포함수(누적 분포함수)를 이해하는 것이 더 쉽게 이해가 된다.
확률밀도함수(PDF)
확률밀도함수(Probability Density Function, PDF)는 연속 확률변수의 분포를 설명하는 함수로, 특정 구간에서 확률변수의 값이 나타날 확률을 나타낸다. PDF는 확률변수가 특정 값을 가질 확률 자체를 나타내지 않고, 그 값 근처의 확률을 표현한다.

f(x) = dF(x) / dx 꼴로 어렵게 생각하지말고 해당 x 의 f(x)는 그 값의 확률을 나타낸다고 생각하자 값은 항상 0 이상이다.
누적분포함수(CDF)
누적분포함수(Cumulative Distribution Function, CDF)는 확률변수 X가 특정 값 x 이하가 될 확률을 나타낸다.
명칭 그대로 "누적" 하여 확률을 나타내는 식이다. 확률 분포함수라고도 한다.

F(x) = P(X ≤ x) 형태로 나타낸다. 당연하게도 x 값은 그 이전값들의 누적값이라서 그렇다. 그래프의 특징으로는 기울기가 음수인 구간이 없다. 즉 x 값이 증가할수록 CDF의 값은 증가하거나 동일하다. 따라서 값 또한 0에서 1 사이에 존재한다.
특징 및 통계학에서의 활용
확률밀도함수(PDF)
1. 기대값 및 분산 계산
평균값 값의 분포 정도를 확인 할 수 있다.
2. 분포의 모양 파악
데이터의 중심 경향성, 퍼짐 정도, 왜곡 등을 파악할 수 있다.
3. 확률밀도의 비교
두 개 이상의 확률분포를 비교할 때 데이터가 어떤 분포에 가까운지, 또는 어떤 변수 간의 관계가 있는지를 분석할 수 있다.
누적분포함수(CDF)
1. 특정 확률 찾기
확률변수가 특정 값 이하가 될 확률을 찾을 수 있다.
2. 신뢰구간 추정
확률변수의 신뢰구간을 추정할 수 있다. 예를 들어, 표본 평균의 95% 신뢰구간을 구하려면, CDF를 사용하여 하위 2.5%와 상위 2.5%의 값을 찾을 수 있다.
마무리
결론적으로는 누적분포함수(CDF)와 확률밀도함수(PDF)의 차이점에 따른 특징을 잘 캐치해서 확률분포를 이해하고 분석하는 데에 적절한 방식을 사용하자
'Machine Learning' 카테고리의 다른 글
| Optimaization/ Lagrange multiplier 라그랑지안 승수법 (0) | 2023.04.09 |
|---|---|
| Optimaization/Pareto Op 파레토 최적화, 프론티어 (0) | 2023.04.09 |
| RV / moment 모멘트; 확률 분포의 특성 (0) | 2023.04.06 |
| RV / standard random variable[Z-score] 표준 확률 변수 (0) | 2023.04.06 |
| RV / non-linear & linear TF 확률 변수 비선형 & 선형 변환 (0) | 2023.04.06 |
