목차
개요
Linear ordinary differential equation(선형 상미분방정식)의 해를 구하는 방식으로 많이 쓰인다. 어렵게 생각하지말고 수학자들이 만든 해를 쉽게 구하는 방식이라고 보면 된다.(수학적으로 유효한 방법을 곁들인)
대학에서는 공업수학으로 빌드업을 해서 기계계열은 제어공학이나 진동공학 등으로 전기전자는 주파수 등으로 열이나 파동방정식을 배울때도 사용이 된다.
그래서 라플라스 변환은 어디에 쓰이는가?
LDE를 기존의 실수 공간에서 풀이가 어려울때 이를 복소공간으로 변환을 시켜 단순하게 만든다.
➡ t - domain 에서의 (예시: 파동에 관련된) 복잡한 미분방정식을 라플라스 변환을 한다.
간단한 공간속에서 계산을 한다.
➡ s - domain 에서 대수 방정식이나 간단한 형태의 미분 방정식으로 계산을 한다.
복소 공간의 결과값을 다시 라플라스 역변환을 통해 기존 공간에서의 해를 얻어낸다.
➡ 변환을 통하여 t - domain 에서의 해를 얻어낸다
한계
오직 LDE에서만 가능하다. Non-LDE는 수치해석 등으로 해결해야한다.
라플라스 변환 조건
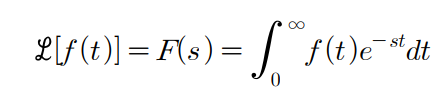

아래에 보이는 식이 만족해야한다.
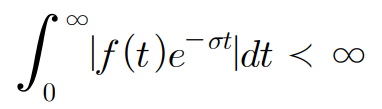
그럼 이 식의 의미는 무엇일까?
위에서 라플라스 변환이 사용되는 과정을 보았을때 t-domain 에서 s-domain으로 옮겨서 풀었던 것을 확인할수 있다. 만약 위의 구간에서 정적분을 하였을시에 수렴이 되지 않는다면 이는 s 에 관한 함수로 나타내지 못하게된다.
f(t)가 위의 구간에서 구간연속(유한한 개수의 불연속점에서 각 불연속점의 좌 우 극한이 모두 유한값을 가질때)이고 그 값이 유한할때 변환이 가능하다. 라고 정리 할 수 있겠다.
라플라스 변환 표

몇번 계산을 하다보면 대강 외워지거나 기억하기 쉽다.
라플라스 변환에 관한 특성
아래 내용들은 특성들이니 따로 설명할것은 없고 미분이나 적분등은 직접한번 해보는것이 좋다.
1. 상수 k에 대한 양변 곱
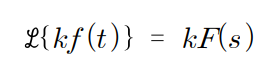
2. 서로 다른 함수의 합과 차는 라플라스 변환의 합과 차와 같다.
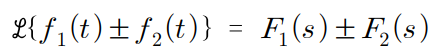
3. 1차 도함수, 미분의 라플라스 변환
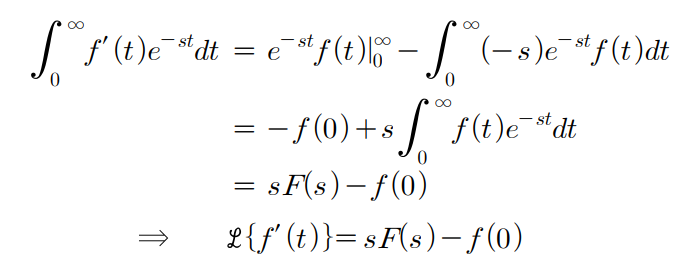
정적분 파트와 적분항 파트로 나눠지는것을 보면 부분적분을 통한것을 확인 할 수 있다. 이해에 도움이 되길
4. n차 도함수, 미분의 라플라스 변환
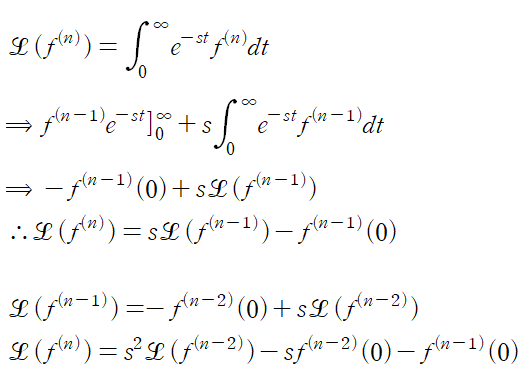
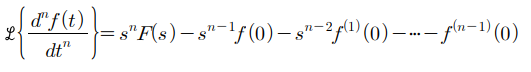
5. 1차 적분의 라플라스 변환
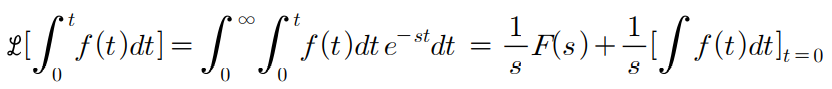
6. n차 적분의 라플라스 변환
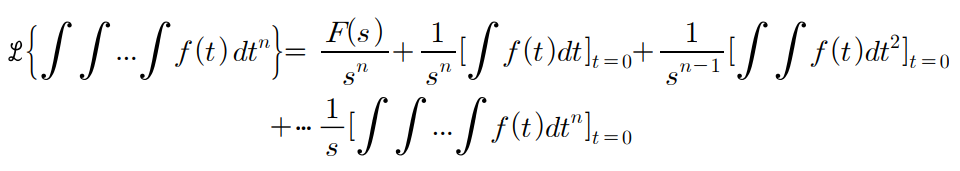
5. 합성곱
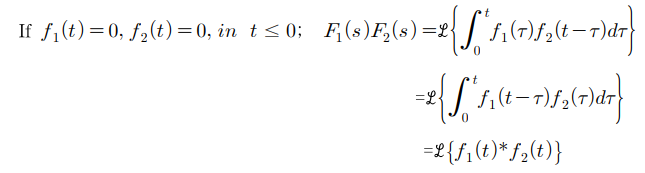
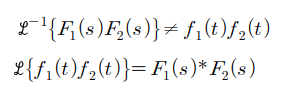
다음 포스팅은 라플라스 변환 에서의 초기값 정리(Initial value theorem)와 최종값 정리(Final value theorem)에 대해서 알아보자.
'Engineering' 카테고리의 다른 글
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
|---|---|
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
| 라플라스 폴 (0) | 2022.09.21 |
| 새로운 카테고리 생성을 하며 (0) | 2022.09.21 |
목차
개요
Linear ordinary differential equation(선형 상미분방정식)의 해를 구하는 방식으로 많이 쓰인다. 어렵게 생각하지말고 수학자들이 만든 해를 쉽게 구하는 방식이라고 보면 된다.(수학적으로 유효한 방법을 곁들인)
대학에서는 공업수학으로 빌드업을 해서 기계계열은 제어공학이나 진동공학 등으로 전기전자는 주파수 등으로 열이나 파동방정식을 배울때도 사용이 된다.
그래서 라플라스 변환은 어디에 쓰이는가?
LDE를 기존의 실수 공간에서 풀이가 어려울때 이를 복소공간으로 변환을 시켜 단순하게 만든다.
➡ t - domain 에서의 (예시: 파동에 관련된) 복잡한 미분방정식을 라플라스 변환을 한다.
간단한 공간속에서 계산을 한다.
➡ s - domain 에서 대수 방정식이나 간단한 형태의 미분 방정식으로 계산을 한다.
복소 공간의 결과값을 다시 라플라스 역변환을 통해 기존 공간에서의 해를 얻어낸다.
➡ 변환을 통하여 t - domain 에서의 해를 얻어낸다
한계
오직 LDE에서만 가능하다. Non-LDE는 수치해석 등으로 해결해야한다.
라플라스 변환 조건
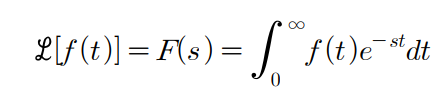

아래에 보이는 식이 만족해야한다.
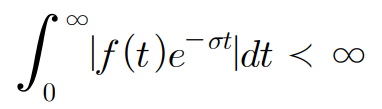
그럼 이 식의 의미는 무엇일까?
위에서 라플라스 변환이 사용되는 과정을 보았을때 t-domain 에서 s-domain으로 옮겨서 풀었던 것을 확인할수 있다. 만약 위의 구간에서 정적분을 하였을시에 수렴이 되지 않는다면 이는 s 에 관한 함수로 나타내지 못하게된다.
f(t)가 위의 구간에서 구간연속(유한한 개수의 불연속점에서 각 불연속점의 좌 우 극한이 모두 유한값을 가질때)이고 그 값이 유한할때 변환이 가능하다. 라고 정리 할 수 있겠다.
라플라스 변환 표

몇번 계산을 하다보면 대강 외워지거나 기억하기 쉽다.
라플라스 변환에 관한 특성
아래 내용들은 특성들이니 따로 설명할것은 없고 미분이나 적분등은 직접한번 해보는것이 좋다.
1. 상수 k에 대한 양변 곱
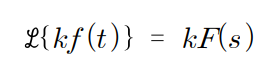
2. 서로 다른 함수의 합과 차는 라플라스 변환의 합과 차와 같다.
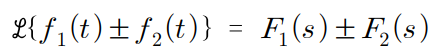
3. 1차 도함수, 미분의 라플라스 변환
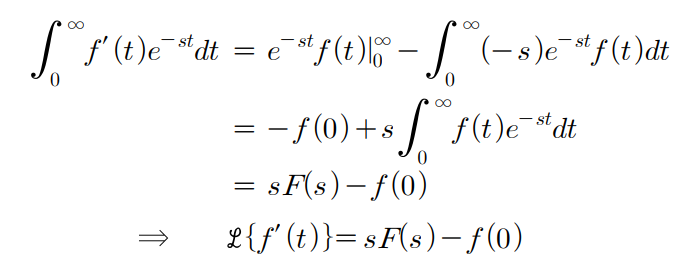
정적분 파트와 적분항 파트로 나눠지는것을 보면 부분적분을 통한것을 확인 할 수 있다. 이해에 도움이 되길
4. n차 도함수, 미분의 라플라스 변환
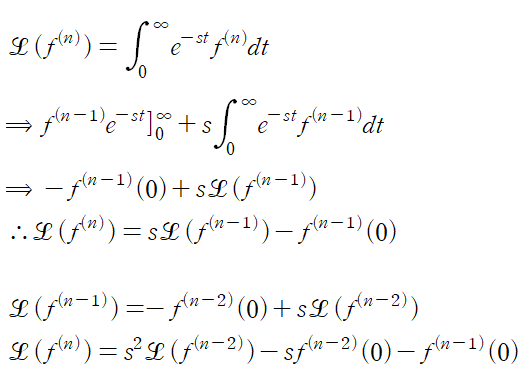
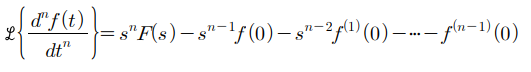
5. 1차 적분의 라플라스 변환
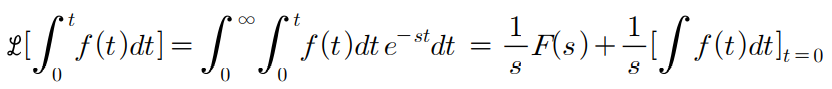
6. n차 적분의 라플라스 변환
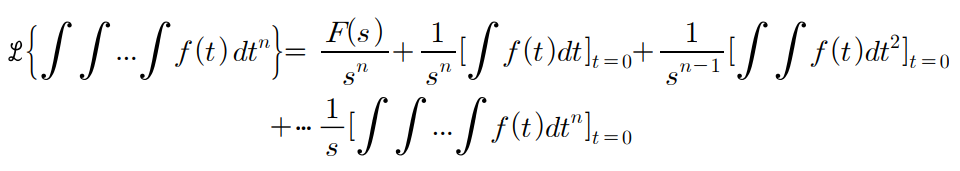
5. 합성곱
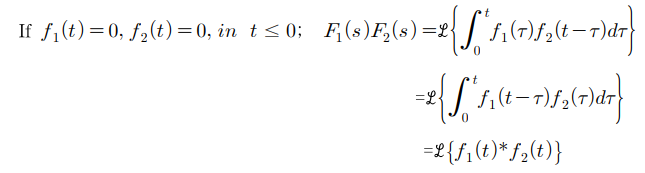
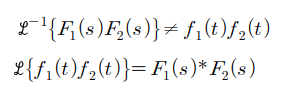
다음 포스팅은 라플라스 변환 에서의 초기값 정리(Initial value theorem)와 최종값 정리(Final value theorem)에 대해서 알아보자.
'Engineering' 카테고리의 다른 글
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
|---|---|
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
| 라플라스 폴 (0) | 2022.09.21 |
| 새로운 카테고리 생성을 하며 (0) | 2022.09.21 |
