목차
개요
본문내용넣기
Pulse
본문내용넣기
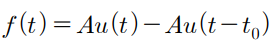
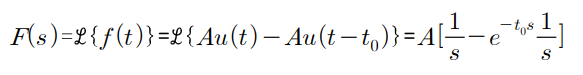
펄스는 동적성을 체크할때 쓴다. 주로 시스템의 input으로 사용됨
ex) 종을 규모 A만큼 t0 만큼 때려라.. But 종을 그렇게 때릴수 있나
Impulse
본문내용넣기
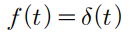
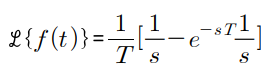
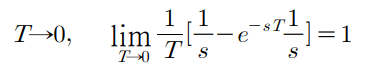
∴ use : transient response, dynamic characteristic
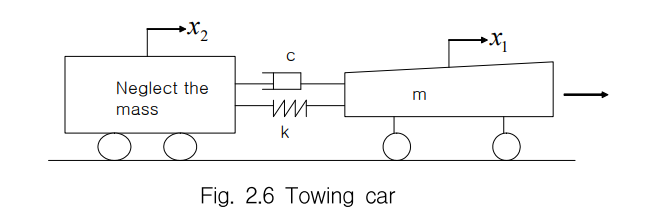
댐퍼에 의한 반력 C : x1dot - x2dot
스프링 : x1-x2
sum F =ma
-c(x1dot-x2dot) - k(x1-x2) = m x1''
laplace : 상미분 방정식
-cx1'+cx2'-kx1+kx2 =mx1''
-c(SX1(s)-x1(0)) +x(SX2(s)-x2(0))-kx1(s)+kx2(s)=
=m(S^2X1(s)-Sx1(0)-x1'(0))
*initaial conditions is zero => 0
-c(SX1(s) +cSX2-kx1 -+kx2- s^2mX1
x1/x2 = cs+k)/(mS2+cS+k) : Transfer function
x2 -> unti step (time domain 1)
X1 = 1/s * cs+k)/(ms^2+cs+k
x1(infi) = lim t>0 s1(t) = lin s>0 SX1(s) = lim s>0 (위의 X1) = 1
https://www.youtube.com/watch?v=s5zO2fuiW7c
Inverse Laplace Transform by Partial-Fraction Expansion
본문내용넣기
중복없는 pole
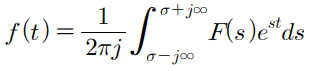
time -> s == transfer function > adaptly Laplace inverse
<Partial - Fraction Expansion
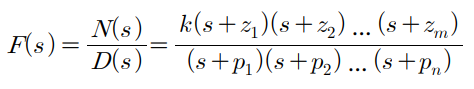
) Roots of the denominator of are real and distinct
Root = Pole (시스템 안정성의 근거)
중복된 Pole 이 없다.
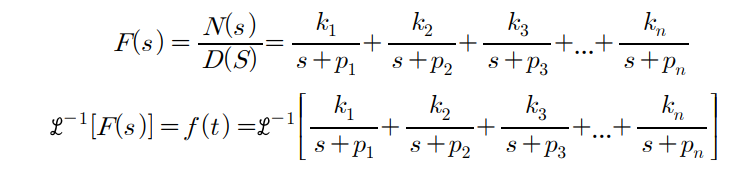
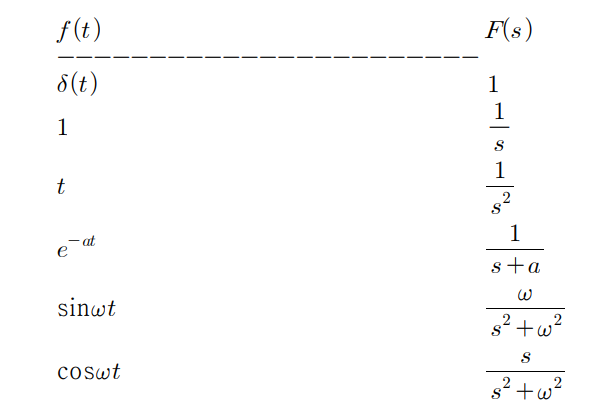
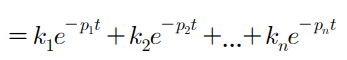
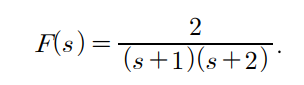
k1/(s+1)+ k2/(s+2)
양변에 s+1 을 곱해준다.
2=k1
2/s+1) s= -2 == k2
F(s) = 2/(s+1)-2(s+2)
f(t) = 2e^-t - 2e^-2t
마무리
중복이 있는 pole 2개이상
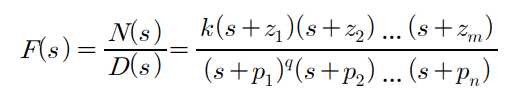
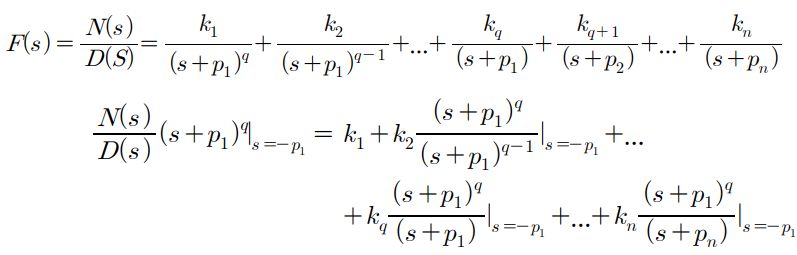
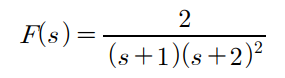
폴 3개 중복 2개
s가있다는건 time domain 에 대한 미분방정식
'Engineering' 카테고리의 다른 글
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
|---|---|
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
| Laplace Transformation 라플라스 변환 (0) | 2022.09.21 |
| 새로운 카테고리 생성을 하며 (0) | 2022.09.21 |
목차
개요
본문내용넣기
Pulse
본문내용넣기
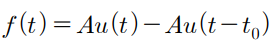
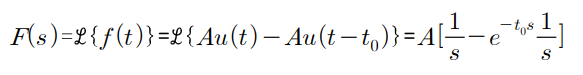
펄스는 동적성을 체크할때 쓴다. 주로 시스템의 input으로 사용됨
ex) 종을 규모 A만큼 t0 만큼 때려라.. But 종을 그렇게 때릴수 있나
Impulse
본문내용넣기
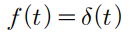
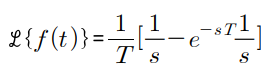
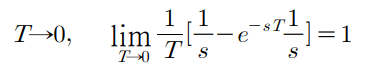
∴ use : transient response, dynamic characteristic

댐퍼에 의한 반력 C : x1dot - x2dot
스프링 : x1-x2
sum F =ma
-c(x1dot-x2dot) - k(x1-x2) = m x1''
laplace : 상미분 방정식
-cx1'+cx2'-kx1+kx2 =mx1''
-c(SX1(s)-x1(0)) +x(SX2(s)-x2(0))-kx1(s)+kx2(s)=
=m(S^2X1(s)-Sx1(0)-x1'(0))
*initaial conditions is zero => 0
-c(SX1(s) +cSX2-kx1 -+kx2- s^2mX1
x1/x2 = cs+k)/(mS2+cS+k) : Transfer function
x2 -> unti step (time domain 1)
X1 = 1/s * cs+k)/(ms^2+cs+k
x1(infi) = lim t>0 s1(t) = lin s>0 SX1(s) = lim s>0 (위의 X1) = 1
https://www.youtube.com/watch?v=s5zO2fuiW7c
Inverse Laplace Transform by Partial-Fraction Expansion
본문내용넣기
중복없는 pole
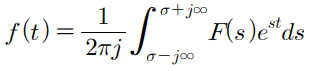
time -> s == transfer function > adaptly Laplace inverse
<Partial - Fraction Expansion
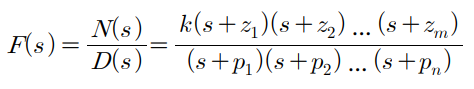
) Roots of the denominator of are real and distinct
Root = Pole (시스템 안정성의 근거)
중복된 Pole 이 없다.
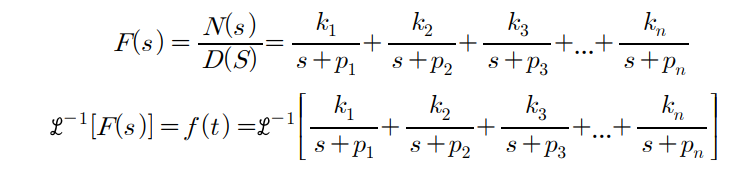
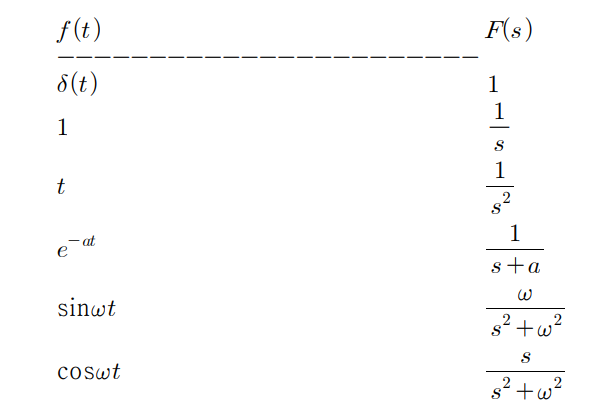
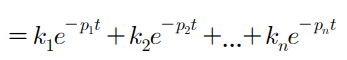
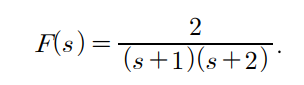
k1/(s+1)+ k2/(s+2)
양변에 s+1 을 곱해준다.
2=k1
2/s+1) s= -2 == k2
F(s) = 2/(s+1)-2(s+2)
f(t) = 2e^-t - 2e^-2t
마무리
중복이 있는 pole 2개이상
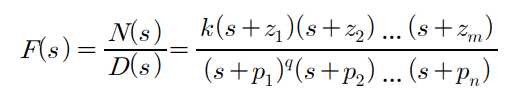
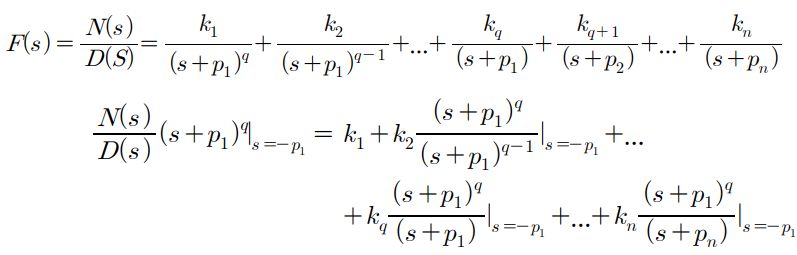
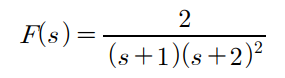
폴 3개 중복 2개
s가있다는건 time domain 에 대한 미분방정식
'Engineering' 카테고리의 다른 글
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
|---|---|
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
| Laplace Transformation 라플라스 변환 (0) | 2022.09.21 |
| 새로운 카테고리 생성을 하며 (0) | 2022.09.21 |
