목차
개요
동역학에서 배웠던 진자운동을 생각해보면
대부분 FBD를 그리고
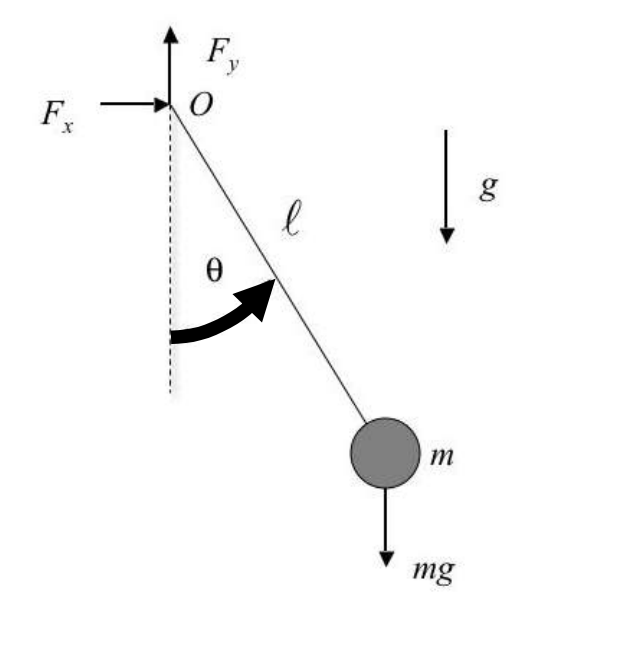
줄의 무게와 중심점에서의 마찰력 탄성등을 전부 무시하고 운동에너지와 위치에너지를 비교하여 계산을 하였었다.
- 뉴턴 2법칙
- 오일러 2법칙
이 두가지를 사용해서
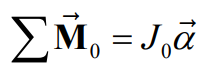
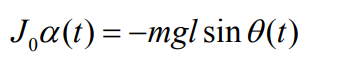
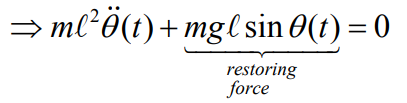
하지만 이 식은 non linear 했기 때문에 우리는 여기서 각이 작을 때
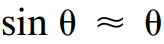
두 값이 비슷해진다는 특성을 사용해서 linear 한 식으로 바꾸어 주었다. (선형화)
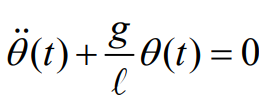
따라서 나온 식 (동역학에서의)
간단한 선형 움직임에 대한 주기 등을 구할 수 있다.
하지만 진동역학을 배우고 나면 선형화 과정을 거치지 않은 값도 확인 할 수 있다.
자유진동 정의
외부의 힘이 가해지지 않은 즉 외력이 있지않을 때의 움직임을 나타낸다.
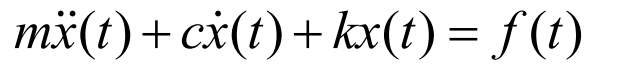
우측 변에 존재 하는 것이 외력 이며 이번 포스팅에서는 항상 0으로 등장 할 것이다.
자유진동 모사 운동방정식에서는
시간에 대한 2차 미분항이 존재하고 초기 속도와 위치에 관한 두가지의 초기 조건이 필요하다.
질량 - 스프링 모델로 자유진동 알아보기
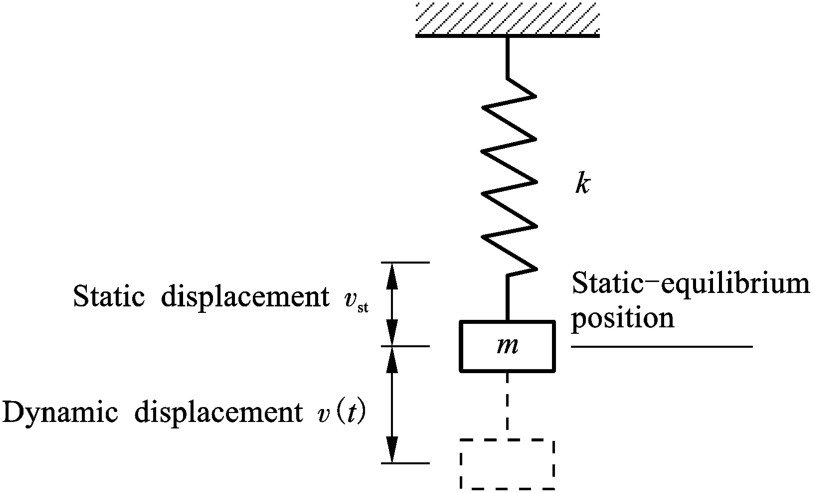
외력이 존재하지 않고 위의 그래프에 맞게 질량과 탄성과의 관계식을 써보면 이렇게 된다.
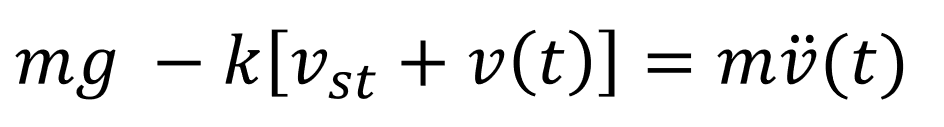
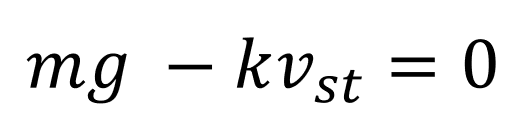
v(t) 가 보기 쉽지않으니 편하게 x(t)로 바꿔주자.
그럼 최종적인 운동 방정식은
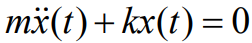
많이 보던 모양이다. 이렇게 나오게 되는데 이때 위 아래로 흔들리는 진자의 흔들림을 어림잡아서 생각해보자 이러한 과정을 추측해 (Approximated solution)이라고 하는데 사인 함수가 주기성이 있으니 이를 이용하여 표현하면
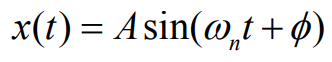

이를 본 식에 대입하기 위해서 2차 도함수로 만들어 운동방정식에 대입해보자.
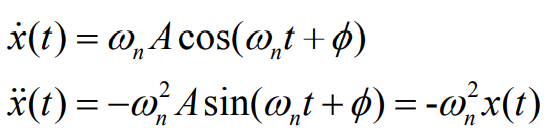
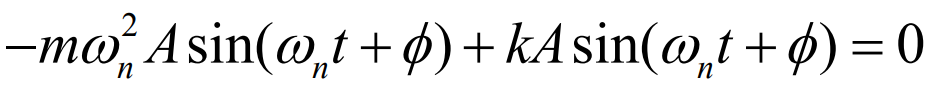
이러한 식을 만족하기 위해서는
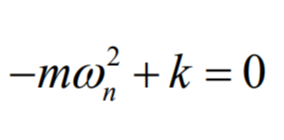
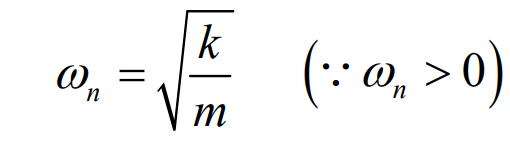
주어진 식을 가지고 소거를 몇번 하게 되면 이 움직임의 진폭이나 위상도 알아낼수 있는데 아까 구했던 도함수에 초기값인 t=0을 대입하여 보면
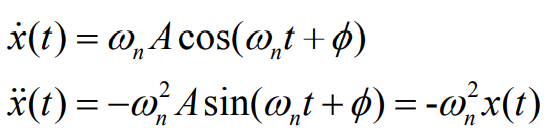
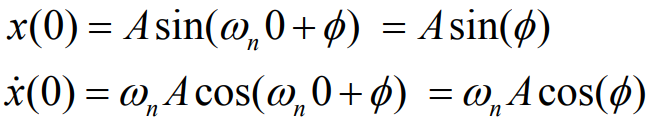
각각을 제곱해서 더해주면 진폭이 나오게 되고 두개로 기울기도 구하게 되면 위상을 구할수 있다.
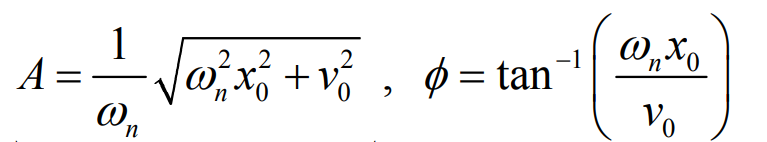
여기서 잠깐 각고유진동수와 고유 진동수에 대해서 구분하고 가자면
각 고유 진동수와 고유 진동수
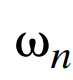
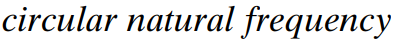
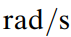
각고유진동수 이고 단위는 rad/s 이다.
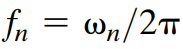
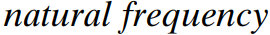
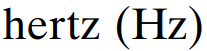
고유진동수 이고 단위는 circle/s Hz 라고도 불린다.
어느정도 차이를 알겠는가??
mass- spring 자유진동 마저 알아보기
아까 구했던 각 고유진동수와 초기조건으로 표현되어있는 진폭이나 위상등을 본 추측해에 대입을 해보자
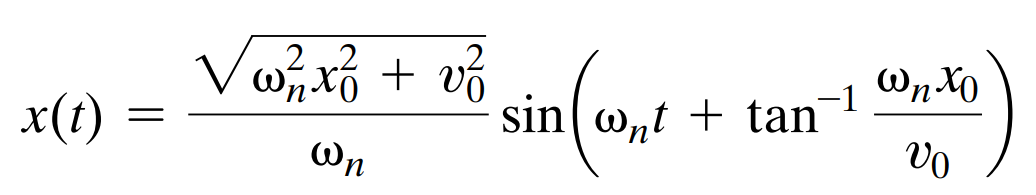
이 해를 free response of the system 이라고 불린다. 즉 자유진동 시스템이고
이러한 mass- spring 자유진동 시스템을 simple harmonic oscillator 또는
undamped single-degree of freedom system(1DOF) 라고 부른다.
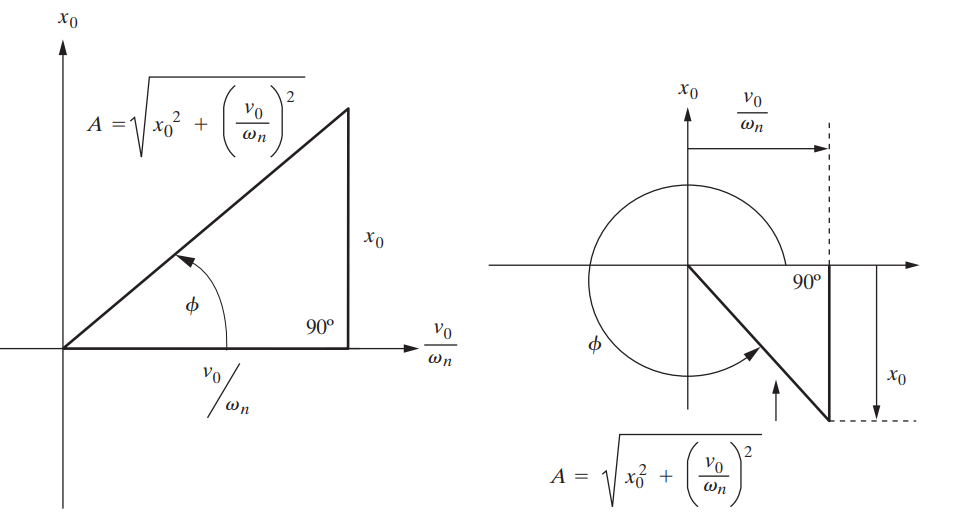
좌측은 양의 초기 위치와 속도에서의 그래프이고 우측은 음의 초기 위치와 양의 속도에서의 그래프이다.
'Engineering' 카테고리의 다른 글
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
|---|---|
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
| 라플라스 폴 (0) | 2022.09.21 |
목차
개요
동역학에서 배웠던 진자운동을 생각해보면
대부분 FBD를 그리고

줄의 무게와 중심점에서의 마찰력 탄성등을 전부 무시하고 운동에너지와 위치에너지를 비교하여 계산을 하였었다.
- 뉴턴 2법칙
- 오일러 2법칙
이 두가지를 사용해서
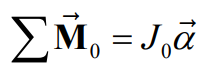
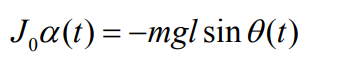
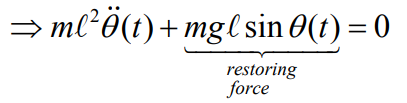
하지만 이 식은 non linear 했기 때문에 우리는 여기서 각이 작을 때
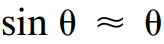
두 값이 비슷해진다는 특성을 사용해서 linear 한 식으로 바꾸어 주었다. (선형화)
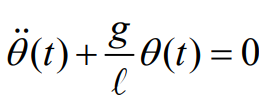
따라서 나온 식 (동역학에서의)
간단한 선형 움직임에 대한 주기 등을 구할 수 있다.
하지만 진동역학을 배우고 나면 선형화 과정을 거치지 않은 값도 확인 할 수 있다.
자유진동 정의
외부의 힘이 가해지지 않은 즉 외력이 있지않을 때의 움직임을 나타낸다.
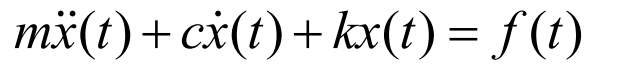
우측 변에 존재 하는 것이 외력 이며 이번 포스팅에서는 항상 0으로 등장 할 것이다.
자유진동 모사 운동방정식에서는
시간에 대한 2차 미분항이 존재하고 초기 속도와 위치에 관한 두가지의 초기 조건이 필요하다.
질량 - 스프링 모델로 자유진동 알아보기

외력이 존재하지 않고 위의 그래프에 맞게 질량과 탄성과의 관계식을 써보면 이렇게 된다.
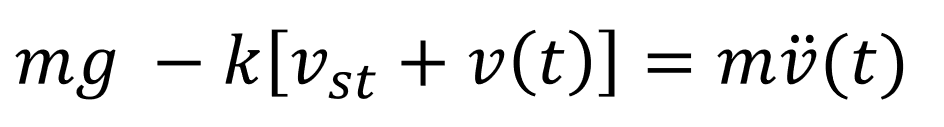
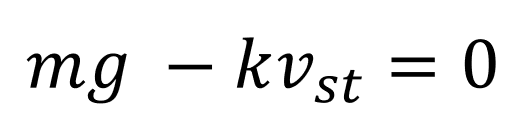
v(t) 가 보기 쉽지않으니 편하게 x(t)로 바꿔주자.
그럼 최종적인 운동 방정식은
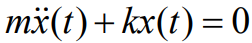
많이 보던 모양이다. 이렇게 나오게 되는데 이때 위 아래로 흔들리는 진자의 흔들림을 어림잡아서 생각해보자 이러한 과정을 추측해 (Approximated solution)이라고 하는데 사인 함수가 주기성이 있으니 이를 이용하여 표현하면
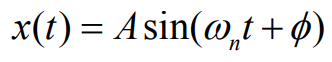

이를 본 식에 대입하기 위해서 2차 도함수로 만들어 운동방정식에 대입해보자.
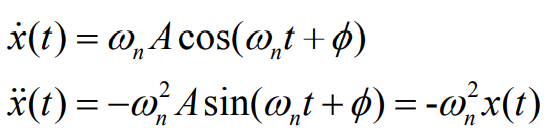
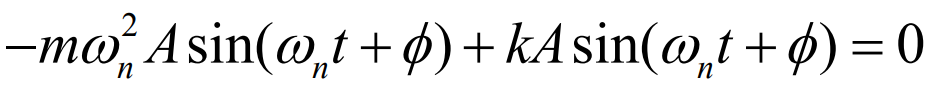
이러한 식을 만족하기 위해서는
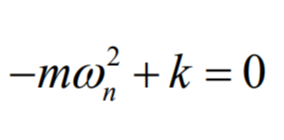
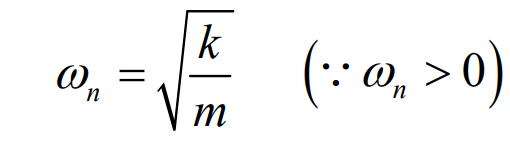
주어진 식을 가지고 소거를 몇번 하게 되면 이 움직임의 진폭이나 위상도 알아낼수 있는데 아까 구했던 도함수에 초기값인 t=0을 대입하여 보면
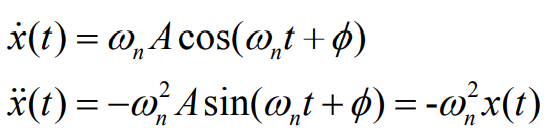
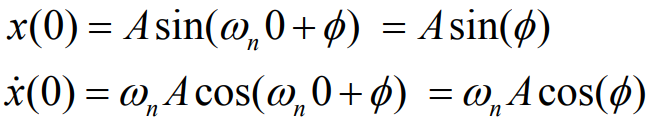
각각을 제곱해서 더해주면 진폭이 나오게 되고 두개로 기울기도 구하게 되면 위상을 구할수 있다.
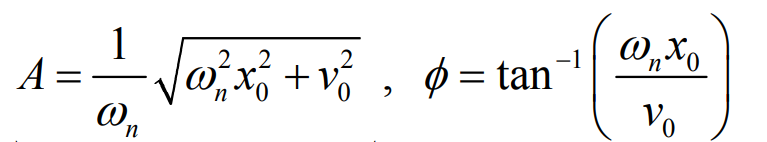
여기서 잠깐 각고유진동수와 고유 진동수에 대해서 구분하고 가자면
각 고유 진동수와 고유 진동수
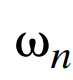
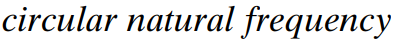
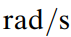
각고유진동수 이고 단위는 rad/s 이다.
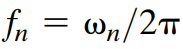
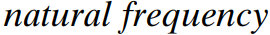
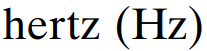
고유진동수 이고 단위는 circle/s Hz 라고도 불린다.
어느정도 차이를 알겠는가??
mass- spring 자유진동 마저 알아보기
아까 구했던 각 고유진동수와 초기조건으로 표현되어있는 진폭이나 위상등을 본 추측해에 대입을 해보자
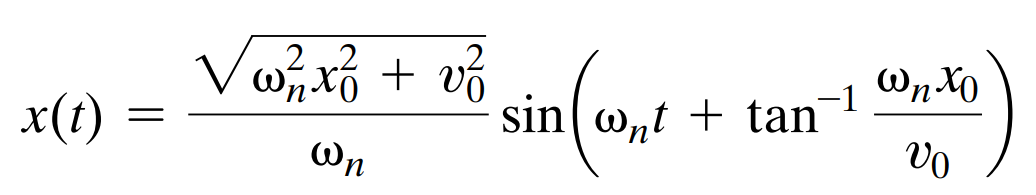
이 해를 free response of the system 이라고 불린다. 즉 자유진동 시스템이고
이러한 mass- spring 자유진동 시스템을 simple harmonic oscillator 또는
undamped single-degree of freedom system(1DOF) 라고 부른다.

좌측은 양의 초기 위치와 속도에서의 그래프이고 우측은 음의 초기 위치와 양의 속도에서의 그래프이다.
'Engineering' 카테고리의 다른 글
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
|---|---|
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
| 라플라스 폴 (0) | 2022.09.21 |
