지난시간의 Classical Lifting line theory의 finite wing의 양 끝점에서의 downwash 값이 무한으로 발산하는 모순점을 해결하는 방식에 대해 알아보자. Thumbnails Credit: Ryoh Ishihara
2022.09.29 - [Engineering] - Lifting-line theory 양력선 이론 자세한 설명 (1)
Lifting-line theory 양력선 이론 자세한 설명 (1)
Vortex Filament, Circulration, Horseshoe Vortex(Bound vortex+ Free trailing vortex), Biot-Savart 정리 들을 통해 Prandtl's Classical Lifting Line을 설명해주는 포스팅 와류 필라멘트, 회전, 말발굽 와..
nstgic3.tistory.com
목차
개요
지난시간의 Classical Lifting line theory의 finite wing의 양 끝점에서의 downwash 값이 무한으로 발산하는 모순점을 해결하는 방식에 대해 알아보자.
Superposition of Horseshoe Vortices
이전 포스팅에서 알게되었던 말발굽 모양의 와류 형상을 무한하게 겹쳐서 양 끝단에서 downwash의 값이 무한으로 발산하는 모순점을 해결하였다.
아래의 그림은 총 3개의 ㄷ 자 형태의 와류가 겹쳐서 만들어지는 와류 집합인데
하나의 모델 내에 존재하는 bound vortex 는 모두 길이가 다르지만 다 같은 직선상에 존재하여 하나의 lifting line을 만들어낸다.
= 어렵게 생각말고 ㄷ 자의 안쪽 부분은 전부 같은 직선에 겹쳤다고 생각해보자
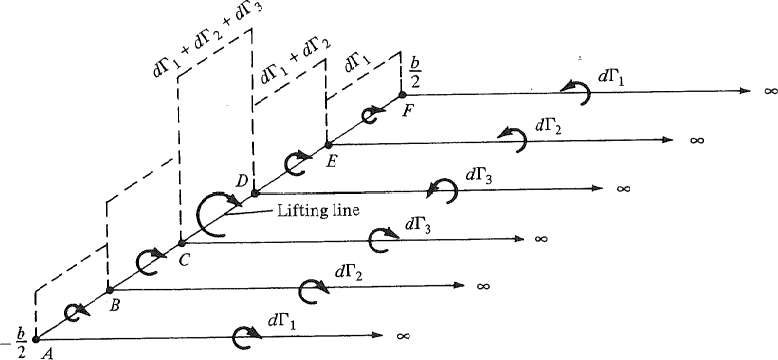
이제 이를 무한개를 겹쳐냈다고 생각해보자
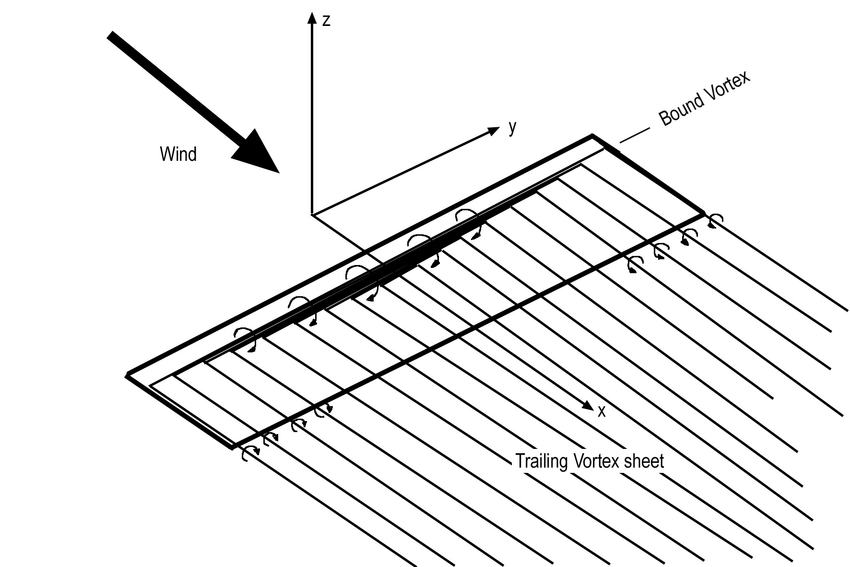
선이 무한개가 겹쳐지면 하나의 2차원 평면이 되지 않겠는가? 이를 Trailing Vortex 로 이루어진 Trailing Vortex sheet 라고 부른다.
이전 포스팅 내에 있던 Biot-Savart Law 에 의해서 여러개의 trailing vortex가 각각의 circulation 을 Lifting line에 만들어낸다.
존재하는 모든 Trailing vortex는 크기가 같다. dΓ 만큼의 값을 가지고 있다.
즉 위의 그림에서 흐르는 BC의 Γ값과 AB의 Γ값의 차이가 dΓ2 임을 이해하고 있어야한다.
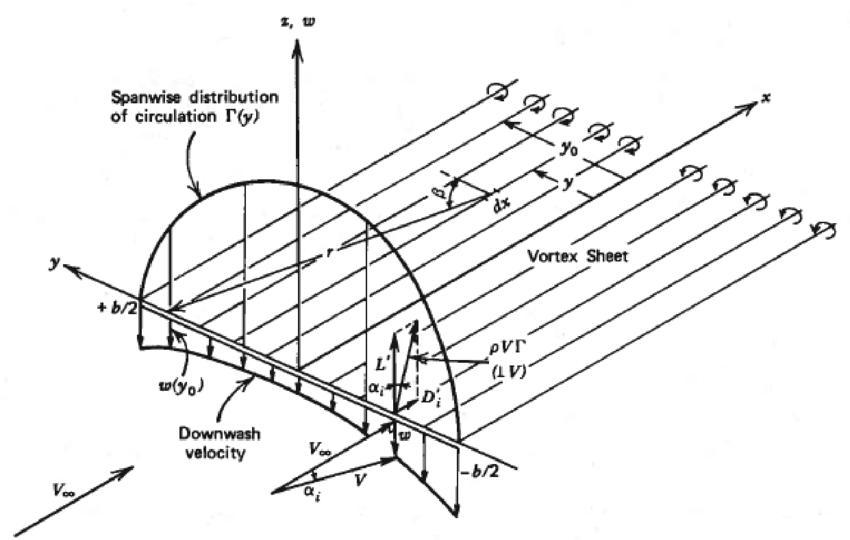
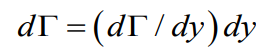
양력선에서의 bound vortex 부분에서의 circulation 의 변화는 우측과 같이
나타낼수 있겠다. 또한 이는 반원 모양의 양력분포도에서의 변화량(기울기)을 나타낸다.
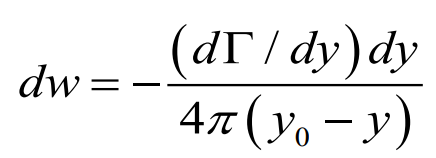
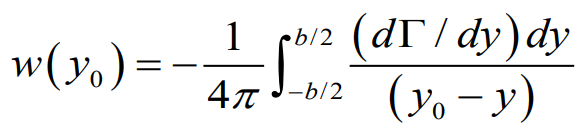
이렇게 나타나는데 위의 trailing vortex의 회전 방향을 y=0을 기준으로 보게 되면 + 부분은 음의 기울기를 가지는 것을 확인 할 수 있는데 이를 이용하여 각 vortex가 Biot-Savart Law에 의한 y0에서의 유도 속도 벡터 방향을 나타낸 것이다.
이전 포스팅에서 알아봤던 작은 각도에서의 유도 받음각도 위의 Superposition of Horseshoe vortex 모델을 대입하여 생각하면
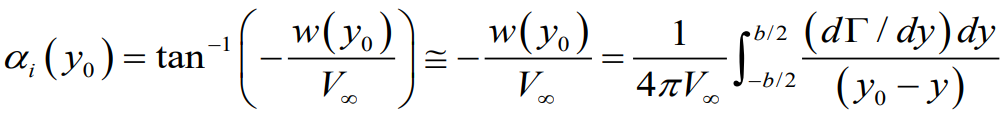
최종적으로 circulation의 분포에 의한 각 지점별 유도 받음각의 수식적 표현이 되겠다.
프란틀 양력선 이론의 기본식 도출하기
0. Lifting line theory 에서 유도된 유도 받음각의 표현법
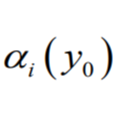
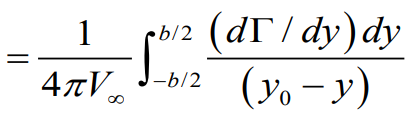
1. Thin airfoil 에서의 Lift slope를 이용한 양력계수 표현
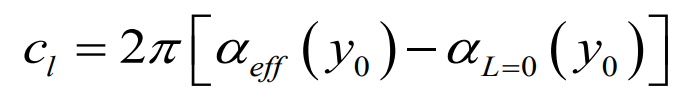
2. 단위길이당 양력 표현식과 Kutta-Joukowski 정리를 이용한 양력계수 표현
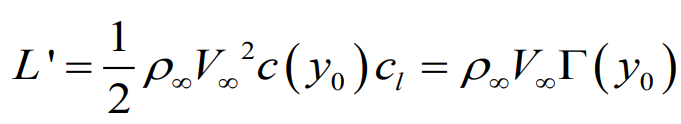
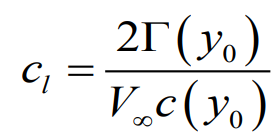
3. 1,2 를 연립하여 유효받음각 표현
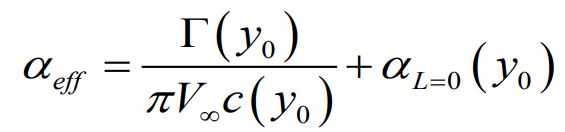
4. 유도 흐름이 유도된 원리를 사용한 유효받음각과 유도받음각을 고려한 실질적 받음각
2022.09.21 - [Engineering] - 내리흐름 Downwash & 유도항력 Induced drag에서 이어지는 개념
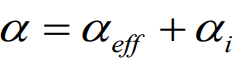
0 과 3의 최종 표현식 대입
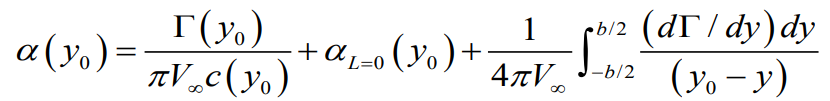
최종적으로 프란틀의 양력선 이론의 기본식 형태가 도출되었다.
양력선 이론이 고려된 양력과 항력
쿠타 주코프스키 정리에서의 지점별 양력 분포
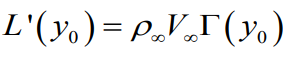
3차원 finite wing 에서의 지점별 양력값과 양력 계수값
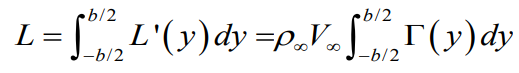
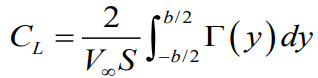
3차원 finite wing 에서의 지점별 유도항력값과 유도항력 계수값
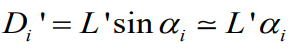
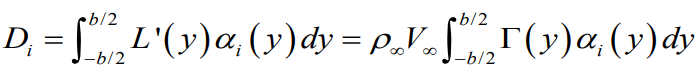
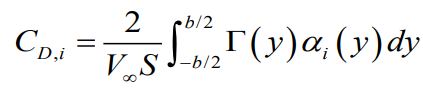
무척 복잡해보이지만 여러가지 수식의 간소화를 위한 조건들이 많이 존재한다.
- 빠르지 않은 속도 (아음속 거동)
- 얇은 날개 두께
- 크지 않은 유도 받음각
- 비점성
- 비압축성
- 모든 지점에서 동등한 circulation 값
짧은 지식이지만 항공우주공학이 공부하는 분야 중 공력해석에 관한 파트는 위의 조건들을 하나씩 적용해제 하면서 거동이 어떻게 바뀌나를 공부하는 분야 인것 같다.
한국어로 인터넷에 제대로 유도 항력이나 받음각에 대해서 정리되어있지 않아서 쓰기 시작하게 되었다.
모든 정보들은 부산대 항공우주공학과 박동훈 교수님의 가르침과 스탠포드에서 오픈해놓은 온라인 자료를 참고했다.
그래서 다음 포스팅에서는 날개의 형상이 다를 경우 지점별 circulation이 달라지고 그에 따라서 양력분포가 달라지게 되는데 어떤 경우가 가장 효율적인지 그 효율에는 어떤 요소가 적용되어있는지 글라이더 날개는 왜이렇게 긴지 에 대해서 알아보자.
2022.10.07 - [Engineering] - Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유)
Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유)
목차 개요 이전 포스팅에서는 여러가지 공식들을 이용하여 만들어낸 Horseshoe vortex라는 가상의 모델을 이용해 Lifting line theory 에 대해서 알아보았다. 그럼 이렇게 만들어진 날개위의 양력분포 형
nstgic3.tistory.com
'Engineering' 카테고리의 다른 글
| 스핏파이어의 날개 형상이 타원형인 이유 (0) | 2022.10.11 |
|---|---|
| Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유) (0) | 2022.10.07 |
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
지난시간의 Classical Lifting line theory의 finite wing의 양 끝점에서의 downwash 값이 무한으로 발산하는 모순점을 해결하는 방식에 대해 알아보자. Thumbnails Credit: Ryoh Ishihara
2022.09.29 - [Engineering] - Lifting-line theory 양력선 이론 자세한 설명 (1)
Lifting-line theory 양력선 이론 자세한 설명 (1)
Vortex Filament, Circulration, Horseshoe Vortex(Bound vortex+ Free trailing vortex), Biot-Savart 정리 들을 통해 Prandtl's Classical Lifting Line을 설명해주는 포스팅 와류 필라멘트, 회전, 말발굽 와..
nstgic3.tistory.com
목차
개요
지난시간의 Classical Lifting line theory의 finite wing의 양 끝점에서의 downwash 값이 무한으로 발산하는 모순점을 해결하는 방식에 대해 알아보자.
Superposition of Horseshoe Vortices
이전 포스팅에서 알게되었던 말발굽 모양의 와류 형상을 무한하게 겹쳐서 양 끝단에서 downwash의 값이 무한으로 발산하는 모순점을 해결하였다.
아래의 그림은 총 3개의 ㄷ 자 형태의 와류가 겹쳐서 만들어지는 와류 집합인데
하나의 모델 내에 존재하는 bound vortex 는 모두 길이가 다르지만 다 같은 직선상에 존재하여 하나의 lifting line을 만들어낸다.
= 어렵게 생각말고 ㄷ 자의 안쪽 부분은 전부 같은 직선에 겹쳤다고 생각해보자

이제 이를 무한개를 겹쳐냈다고 생각해보자

선이 무한개가 겹쳐지면 하나의 2차원 평면이 되지 않겠는가? 이를 Trailing Vortex 로 이루어진 Trailing Vortex sheet 라고 부른다.
이전 포스팅 내에 있던 Biot-Savart Law 에 의해서 여러개의 trailing vortex가 각각의 circulation 을 Lifting line에 만들어낸다.
존재하는 모든 Trailing vortex는 크기가 같다. dΓ 만큼의 값을 가지고 있다.
즉 위의 그림에서 흐르는 BC의 Γ값과 AB의 Γ값의 차이가 dΓ2 임을 이해하고 있어야한다.

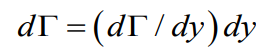
양력선에서의 bound vortex 부분에서의 circulation 의 변화는 우측과 같이
나타낼수 있겠다. 또한 이는 반원 모양의 양력분포도에서의 변화량(기울기)을 나타낸다.
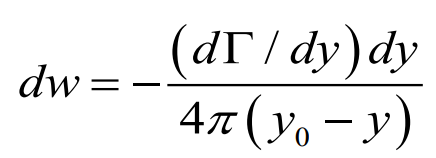
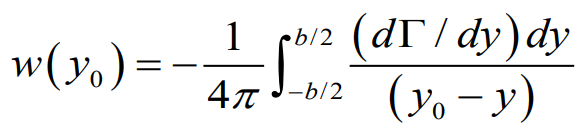
이렇게 나타나는데 위의 trailing vortex의 회전 방향을 y=0을 기준으로 보게 되면 + 부분은 음의 기울기를 가지는 것을 확인 할 수 있는데 이를 이용하여 각 vortex가 Biot-Savart Law에 의한 y0에서의 유도 속도 벡터 방향을 나타낸 것이다.
이전 포스팅에서 알아봤던 작은 각도에서의 유도 받음각도 위의 Superposition of Horseshoe vortex 모델을 대입하여 생각하면
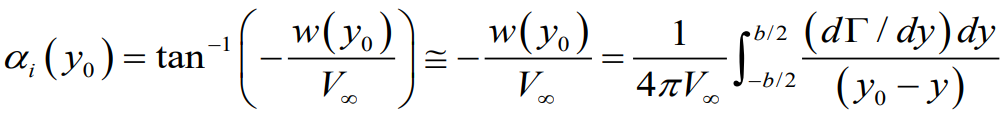
최종적으로 circulation의 분포에 의한 각 지점별 유도 받음각의 수식적 표현이 되겠다.
프란틀 양력선 이론의 기본식 도출하기
0. Lifting line theory 에서 유도된 유도 받음각의 표현법
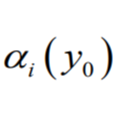
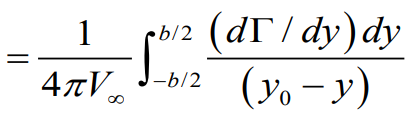
1. Thin airfoil 에서의 Lift slope를 이용한 양력계수 표현
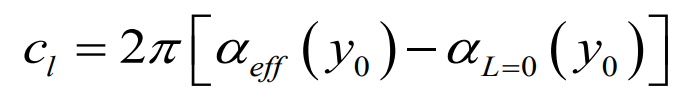
2. 단위길이당 양력 표현식과 Kutta-Joukowski 정리를 이용한 양력계수 표현
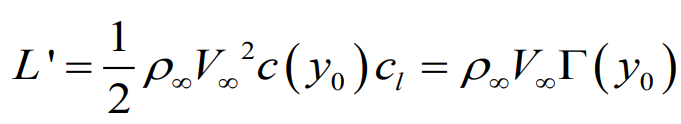
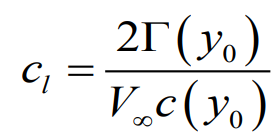
3. 1,2 를 연립하여 유효받음각 표현
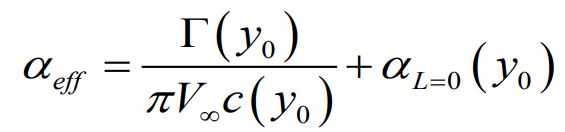
4. 유도 흐름이 유도된 원리를 사용한 유효받음각과 유도받음각을 고려한 실질적 받음각
2022.09.21 - [Engineering] - 내리흐름 Downwash & 유도항력 Induced drag에서 이어지는 개념
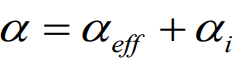
0 과 3의 최종 표현식 대입
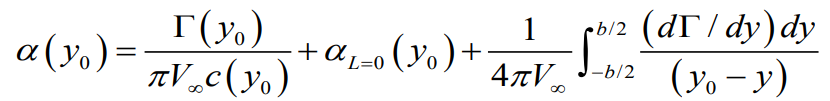
최종적으로 프란틀의 양력선 이론의 기본식 형태가 도출되었다.
양력선 이론이 고려된 양력과 항력
쿠타 주코프스키 정리에서의 지점별 양력 분포
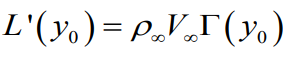
3차원 finite wing 에서의 지점별 양력값과 양력 계수값
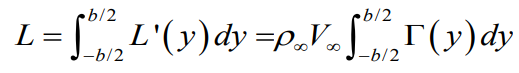
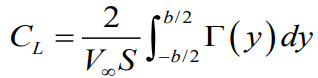
3차원 finite wing 에서의 지점별 유도항력값과 유도항력 계수값
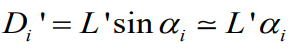
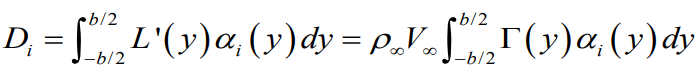
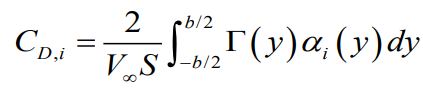
무척 복잡해보이지만 여러가지 수식의 간소화를 위한 조건들이 많이 존재한다.
- 빠르지 않은 속도 (아음속 거동)
- 얇은 날개 두께
- 크지 않은 유도 받음각
- 비점성
- 비압축성
- 모든 지점에서 동등한 circulation 값
짧은 지식이지만 항공우주공학이 공부하는 분야 중 공력해석에 관한 파트는 위의 조건들을 하나씩 적용해제 하면서 거동이 어떻게 바뀌나를 공부하는 분야 인것 같다.
한국어로 인터넷에 제대로 유도 항력이나 받음각에 대해서 정리되어있지 않아서 쓰기 시작하게 되었다.
모든 정보들은 부산대 항공우주공학과 박동훈 교수님의 가르침과 스탠포드에서 오픈해놓은 온라인 자료를 참고했다.
그래서 다음 포스팅에서는 날개의 형상이 다를 경우 지점별 circulation이 달라지고 그에 따라서 양력분포가 달라지게 되는데 어떤 경우가 가장 효율적인지 그 효율에는 어떤 요소가 적용되어있는지 글라이더 날개는 왜이렇게 긴지 에 대해서 알아보자.
2022.10.07 - [Engineering] - Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유)
Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유)
목차 개요 이전 포스팅에서는 여러가지 공식들을 이용하여 만들어낸 Horseshoe vortex라는 가상의 모델을 이용해 Lifting line theory 에 대해서 알아보았다. 그럼 이렇게 만들어진 날개위의 양력분포 형
nstgic3.tistory.com
'Engineering' 카테고리의 다른 글
| 스핏파이어의 날개 형상이 타원형인 이유 (0) | 2022.10.11 |
|---|---|
| Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유) (0) | 2022.10.07 |
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
