목차
개요
지난번 타원형 양력분포의 수식들과 그때의 특징 그리고 AR비의 개념을 도입시켜서 유도항력과 AR비와의 관계를 보았는데 이번 포스팅에서는 특별 케이스인 타원형 양력분포가 아닌 General 한 형상에서의 양력분포도에 대해서 알아보자.
General Lift Distribution을 위한 푸리에 계수 구하기
먼저 타원형 양력분포 일때의 타원의 일반방정식에서 도출된 지점별 양력분포값을 나타내보자
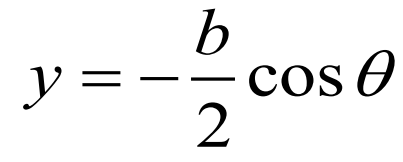
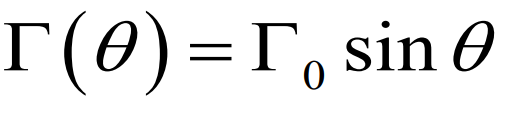
이 값을 일반적인 양력 분포로 이끌어내기 위해서 먼저 각 지점을 N개로 나누어 기함수인 sin 형태로 가정하고
기함수인 이유는 동체의 body를 y=0이라고 두었을때 좌우로 평형한 힘이 주어지기 때문이다.
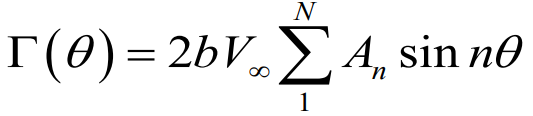
이를 푸리에 사인 급수를 통해 표현해보자면
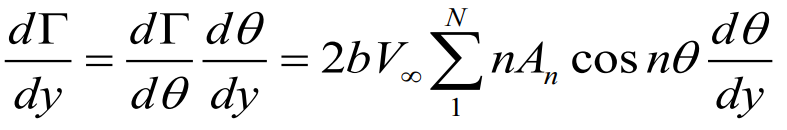
또한 이 공식도 Prandtl`s lifting theory 를 만족하기 때문에 각 지점별 받음각을 표현해보면
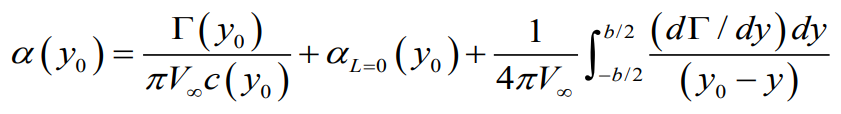
뒤의 적분 내부의 식을 위에서 구한 푸리에 사인 급수를 사용하여 치환하여 표현하고 적분을 진행하면 아래와같은 결과값이 나오게된다.
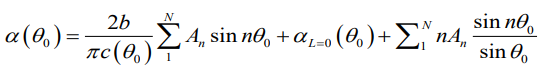
위의 공식에서 알고있는 값들은 날개의 길이 b , b=0 지점에서의 받음각, b=0 지점에서의 chord 길이 총 3개이고 모르는 값들은 시그마 내에 있는 N개의 An 요소들이다.
지금 우리가 구하고자 하는것은 각 지점의 유도받음각이 일정한 타원형 양력분포의 경우가 아닌 각각의 지점에서 다른 값을 가지는 일반적인 경우를 상정하는 것이기 때문에 우리는 위에 있는 theta0 즉 b=0지점에서의 받음각 뿐만 아니라 Span 방향으로 N개의 미소지점으로 나누어서 이를 구해보려고 한다.
따라서 이러한 N개의 spanwise stations로 인해 나오는 N개의 받음각 식과 각 식에 있는 시그마 내에 있는 N개의 An 요소들
이 도출되게 되는데
어? N개의 식과 N개의 미지요소 N algebraic Eqs N unknowns
바로 행렬을 때려보자
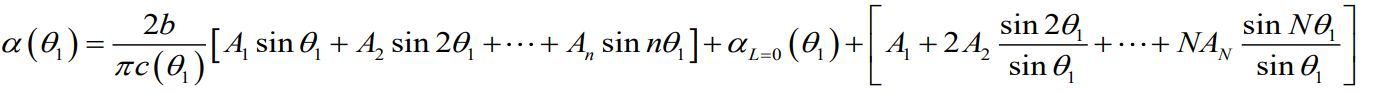
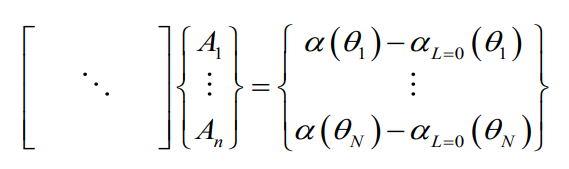
그럼 우리는 이제 미지의 An 요소들을 모두 구할 수 있게 되고 이는 각 지점별 받음각을 구할 수 있게 되었다는 뜻이다.
그럼 우리는 앞으로 사용될 여러 요소들의 푸리에 계수에 대해서 구하게 된것이다.
*설명이 미흡하거나 틀렸다면 댓글로 부탁드립니다.
General Lift DIstribution에서 양력계수, 유도 받음각, 유도 항력 성분 구하기
양력계수의 경우
Circulation 값을 알고 있을때 유한날개에서의 양력계수는
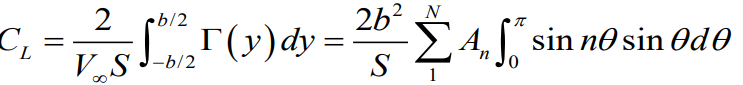
이러한 형태를 띄고 있었다.
만일 N이 1인 즉 좌측에서 첫번째 성분을 꺼내보면
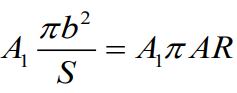
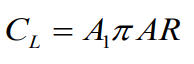
양력계수가 위에서 구한 푸리에 변환의 푸리에 계수에 따라서 달라짐을 확인할 수 있다.
(하지만 그 계수 이미 구했죠? 그럼 지점별 양력계수는 구해졌다)
유도받음각의 경우
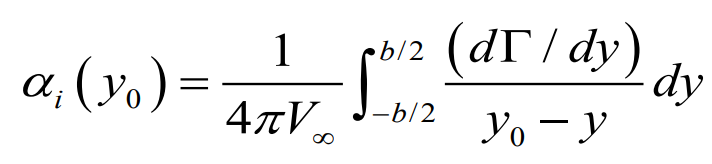
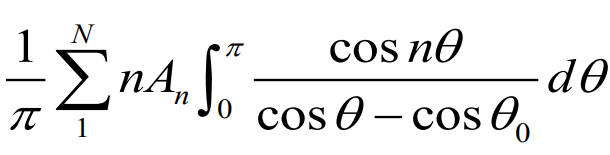
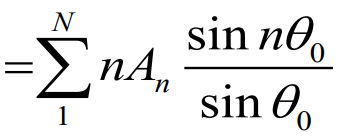
최종적으로 유도 받음각의 크기의 값도 표현이 가능하다. 물론 이것도 푸리에 계수로 표현이 된다.
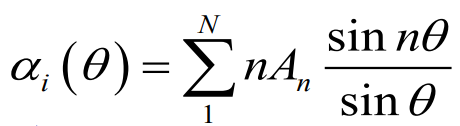
유도 항력계수의 경우
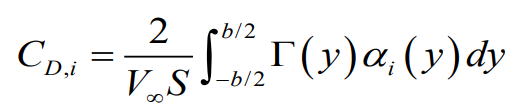
- General Lift Distribution 에서의 Circulation 값
- General Lift Distribution 에서의 유도 받음각 값
을 치환해준다. 그럼 아래와 같은 식이 나오는데 같은 구간끼리의 시그마 곱 성질을 이용하여 식을 간단히 해주면
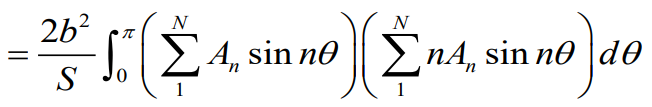
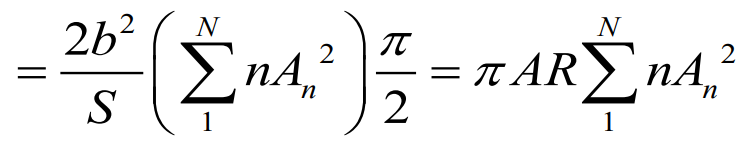
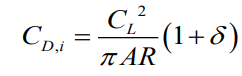
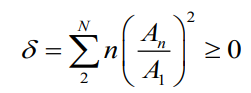
항상 타원형보다 유도항력계수가 크다.
새로운 계수 도입 : span efficiency effect
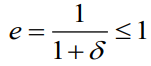
계수를 이용한 일반적인 양력분포에서 유도항력 계수
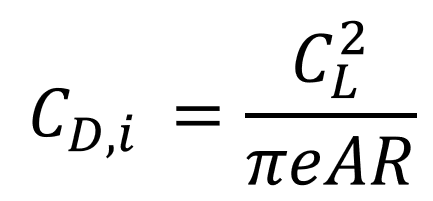
위의 식에서 최소의 유도항력을 가지기 위해서는 span efficiency effect가 최대가 되어야하고 e가 최대가 될때는 δ=0 이될때 즉 타원형 양력분포를 이룰때 이므로
the lift distribution which yields minimum induced drag is elliptical lift distribution
유도항력이 최소가 되는 지점은 양력이 타원형으로 분포가 되어있어야한다.
타원형 양력분포의 조건
타원형 양력분포의 조건으로는
- geometric twist 와 aerodynamic twist가 없어야한다.
- 모든 지점에서 유효 받음각이 같아야한다.
- 모든 지점에서 양력 계수가 같아야한다.
- c/4 지점에 모든 airfoil의 span c/4 지점이 모여있어야한다. 즉 날개 형상도 타원형 이어야한다.
타원형 양력분포를 가지는 스핏파이어

스핏파이어의 날개 형상이 딱 위의 조건에 부합하여 면적대비 효율 좋은 양력을 만들어 내었고 그렇기에 2차 세계대전에서 영국군의 주력 전투기로 명성을 떨쳤다.
여담으로 빠르고 기동성이 뛰어난데다 명품 기관총인 브라우닝을 달고 중요임무를 수행하는 등 2차세계 대전의 승리에 공헌하였다. 한국전쟁 초반에도 조금 활약했다고 알고있다.
그럼 이때 당시의 모든 전투기들의 날개는 왜 스핏파이어처럼 만들지 않았을까?
현실적인 이유
타원형 날개는 제작하기에 어려워서 제작비가 비싸다.
직사각형 모양 ➡ 유도 항력 관점에서 안좋다.
타원형과 비슷하면서 제작이 쉬운 형태 ➡ 테이퍼 형태
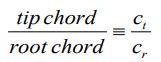
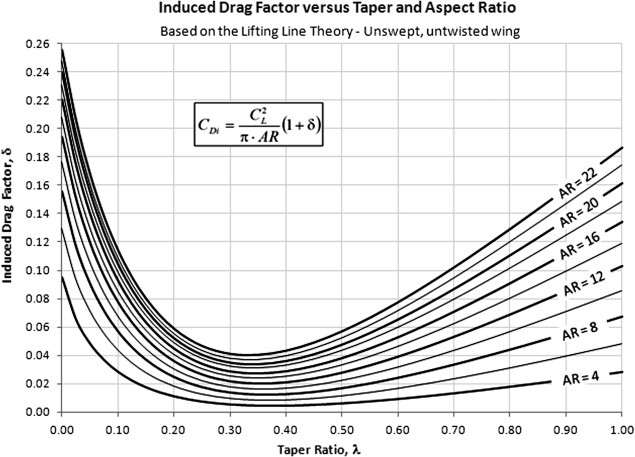
위의 그래프를 보면 Taper 된 정도 즉 Taper Ratio 가 얼마나 유도 항력 계수의 변화에 기여하는지를 계산해 볼 수 있는데 하단에 쓰여있는 Taper Ratio 는 일정 이상의 비율이 되면 비율이 커져도 유도 항력 계수가 줄어들지는 않고 오히려 조금 커지는 것을 확인 할 수있다.
또한 Induced Drag Factor의 증가량이 AR의 증가량에 비해서 크지 않는것을 확인 할 수있는데
자세한 내용은 다음 포스팅에서 다룰것이지만 AR의 상승이 항력 유도 계수의 감소에 큰 영향을 준 다는 사실을 기억하는가?
간단히 말하자면 AR의 증가에 따라 증가하는 유도항력요소의 정도보다 AR 증가로 감소되는 유도항력계수의 정도가 더 커서 AR이 더 클수록 낮은 유도항력계수를 가진다.
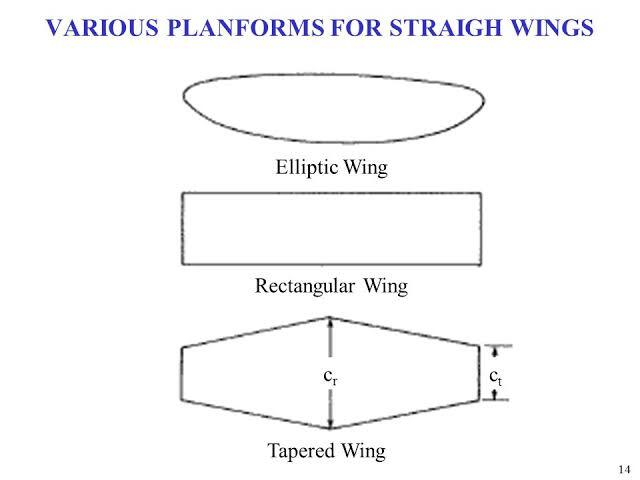
아무래도 둥글게 만드는 것보다 직선형으로 제작을 하는 것이 대량생산에 유용하기 때문에 미군에서는 타원형 날개보다는 떨어지지만 직사각형 날개보다는 효율적인 형태인 테이퍼드 윙을 달고 p51 머스탱을 설계하여 생산력과 양력효율 모두를 잡았다.


여담으로 나치독일에 대적하여 높은 기동력과 폭격기의 엄호를 위해 긴 항속거리를 목표에 두고 설계를 했었는데 이는 무척 성공적이었고 머스탱의 은빛날개가 심볼이 되었다고 한다. 또한 한국공군이 최초로 사용한 전투기이기도하다.
'Engineering' 카테고리의 다른 글
| 진보한 양력모델 Lifting-Surface Method (0) | 2022.10.11 |
|---|---|
| AR비 그리고 Span loading (0) | 2022.10.11 |
| Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유) (0) | 2022.10.07 |
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
목차
개요
지난번 타원형 양력분포의 수식들과 그때의 특징 그리고 AR비의 개념을 도입시켜서 유도항력과 AR비와의 관계를 보았는데 이번 포스팅에서는 특별 케이스인 타원형 양력분포가 아닌 General 한 형상에서의 양력분포도에 대해서 알아보자.
General Lift Distribution을 위한 푸리에 계수 구하기
먼저 타원형 양력분포 일때의 타원의 일반방정식에서 도출된 지점별 양력분포값을 나타내보자
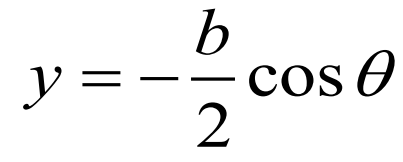
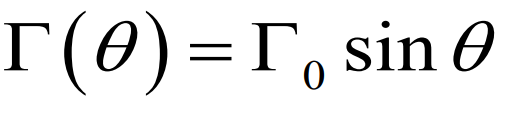
이 값을 일반적인 양력 분포로 이끌어내기 위해서 먼저 각 지점을 N개로 나누어 기함수인 sin 형태로 가정하고
기함수인 이유는 동체의 body를 y=0이라고 두었을때 좌우로 평형한 힘이 주어지기 때문이다.
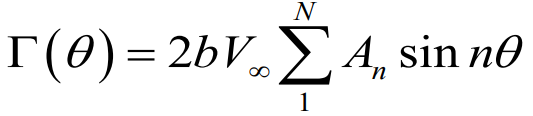
이를 푸리에 사인 급수를 통해 표현해보자면
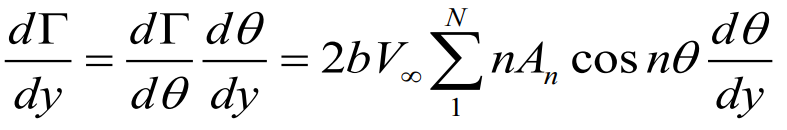
또한 이 공식도 Prandtl`s lifting theory 를 만족하기 때문에 각 지점별 받음각을 표현해보면
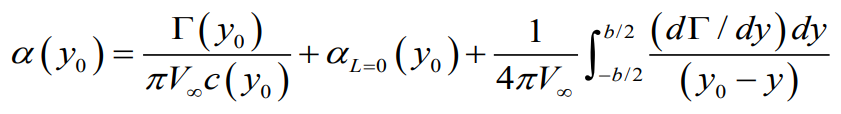
뒤의 적분 내부의 식을 위에서 구한 푸리에 사인 급수를 사용하여 치환하여 표현하고 적분을 진행하면 아래와같은 결과값이 나오게된다.
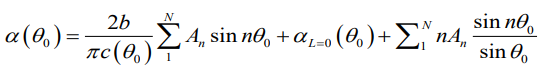
위의 공식에서 알고있는 값들은 날개의 길이 b , b=0 지점에서의 받음각, b=0 지점에서의 chord 길이 총 3개이고 모르는 값들은 시그마 내에 있는 N개의 An 요소들이다.
지금 우리가 구하고자 하는것은 각 지점의 유도받음각이 일정한 타원형 양력분포의 경우가 아닌 각각의 지점에서 다른 값을 가지는 일반적인 경우를 상정하는 것이기 때문에 우리는 위에 있는 theta0 즉 b=0지점에서의 받음각 뿐만 아니라 Span 방향으로 N개의 미소지점으로 나누어서 이를 구해보려고 한다.
따라서 이러한 N개의 spanwise stations로 인해 나오는 N개의 받음각 식과 각 식에 있는 시그마 내에 있는 N개의 An 요소들
이 도출되게 되는데
어? N개의 식과 N개의 미지요소 N algebraic Eqs N unknowns
바로 행렬을 때려보자
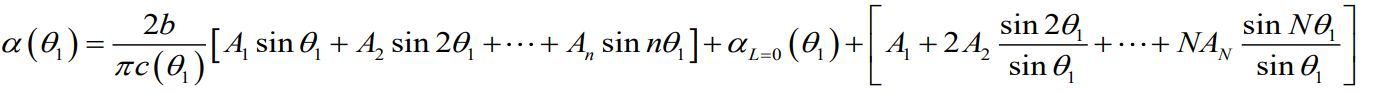
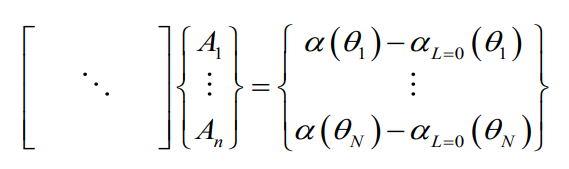
그럼 우리는 이제 미지의 An 요소들을 모두 구할 수 있게 되고 이는 각 지점별 받음각을 구할 수 있게 되었다는 뜻이다.
그럼 우리는 앞으로 사용될 여러 요소들의 푸리에 계수에 대해서 구하게 된것이다.
*설명이 미흡하거나 틀렸다면 댓글로 부탁드립니다.
General Lift DIstribution에서 양력계수, 유도 받음각, 유도 항력 성분 구하기
양력계수의 경우
Circulation 값을 알고 있을때 유한날개에서의 양력계수는
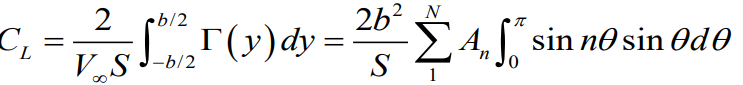
이러한 형태를 띄고 있었다.
만일 N이 1인 즉 좌측에서 첫번째 성분을 꺼내보면
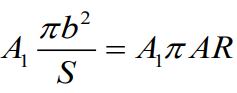
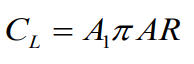
양력계수가 위에서 구한 푸리에 변환의 푸리에 계수에 따라서 달라짐을 확인할 수 있다.
(하지만 그 계수 이미 구했죠? 그럼 지점별 양력계수는 구해졌다)
유도받음각의 경우
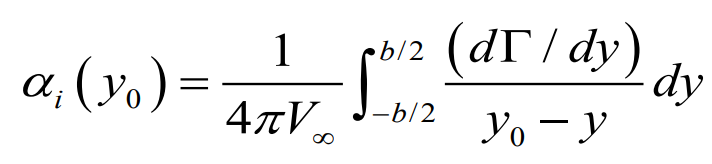
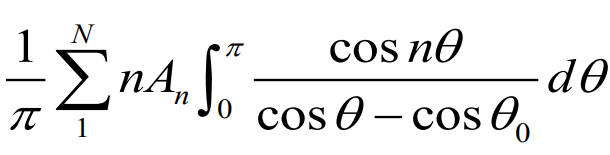
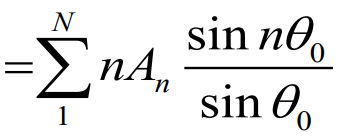
최종적으로 유도 받음각의 크기의 값도 표현이 가능하다. 물론 이것도 푸리에 계수로 표현이 된다.
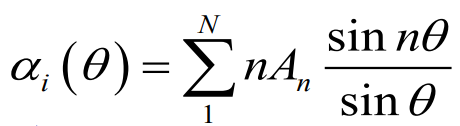
유도 항력계수의 경우
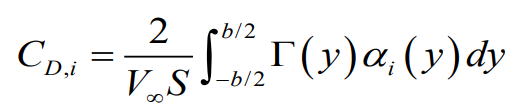
- General Lift Distribution 에서의 Circulation 값
- General Lift Distribution 에서의 유도 받음각 값
을 치환해준다. 그럼 아래와 같은 식이 나오는데 같은 구간끼리의 시그마 곱 성질을 이용하여 식을 간단히 해주면
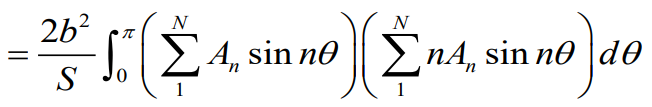
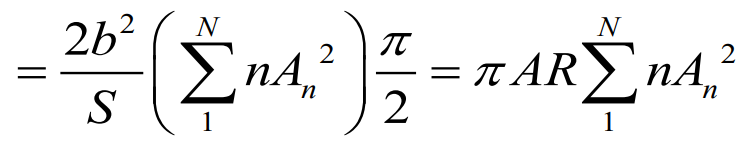
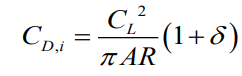
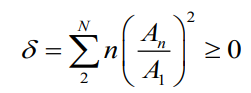
항상 타원형보다 유도항력계수가 크다.
새로운 계수 도입 : span efficiency effect
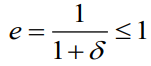
계수를 이용한 일반적인 양력분포에서 유도항력 계수
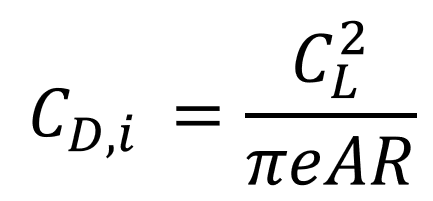
위의 식에서 최소의 유도항력을 가지기 위해서는 span efficiency effect가 최대가 되어야하고 e가 최대가 될때는 δ=0 이될때 즉 타원형 양력분포를 이룰때 이므로
the lift distribution which yields minimum induced drag is elliptical lift distribution
유도항력이 최소가 되는 지점은 양력이 타원형으로 분포가 되어있어야한다.
타원형 양력분포의 조건
타원형 양력분포의 조건으로는
- geometric twist 와 aerodynamic twist가 없어야한다.
- 모든 지점에서 유효 받음각이 같아야한다.
- 모든 지점에서 양력 계수가 같아야한다.
- c/4 지점에 모든 airfoil의 span c/4 지점이 모여있어야한다. 즉 날개 형상도 타원형 이어야한다.
타원형 양력분포를 가지는 스핏파이어

스핏파이어의 날개 형상이 딱 위의 조건에 부합하여 면적대비 효율 좋은 양력을 만들어 내었고 그렇기에 2차 세계대전에서 영국군의 주력 전투기로 명성을 떨쳤다.
여담으로 빠르고 기동성이 뛰어난데다 명품 기관총인 브라우닝을 달고 중요임무를 수행하는 등 2차세계 대전의 승리에 공헌하였다. 한국전쟁 초반에도 조금 활약했다고 알고있다.
그럼 이때 당시의 모든 전투기들의 날개는 왜 스핏파이어처럼 만들지 않았을까?
현실적인 이유
타원형 날개는 제작하기에 어려워서 제작비가 비싸다.
직사각형 모양 ➡ 유도 항력 관점에서 안좋다.
타원형과 비슷하면서 제작이 쉬운 형태 ➡ 테이퍼 형태
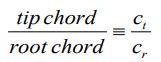

위의 그래프를 보면 Taper 된 정도 즉 Taper Ratio 가 얼마나 유도 항력 계수의 변화에 기여하는지를 계산해 볼 수 있는데 하단에 쓰여있는 Taper Ratio 는 일정 이상의 비율이 되면 비율이 커져도 유도 항력 계수가 줄어들지는 않고 오히려 조금 커지는 것을 확인 할 수있다.
또한 Induced Drag Factor의 증가량이 AR의 증가량에 비해서 크지 않는것을 확인 할 수있는데
자세한 내용은 다음 포스팅에서 다룰것이지만 AR의 상승이 항력 유도 계수의 감소에 큰 영향을 준 다는 사실을 기억하는가?
간단히 말하자면 AR의 증가에 따라 증가하는 유도항력요소의 정도보다 AR 증가로 감소되는 유도항력계수의 정도가 더 커서 AR이 더 클수록 낮은 유도항력계수를 가진다.

아무래도 둥글게 만드는 것보다 직선형으로 제작을 하는 것이 대량생산에 유용하기 때문에 미군에서는 타원형 날개보다는 떨어지지만 직사각형 날개보다는 효율적인 형태인 테이퍼드 윙을 달고 p51 머스탱을 설계하여 생산력과 양력효율 모두를 잡았다.


여담으로 나치독일에 대적하여 높은 기동력과 폭격기의 엄호를 위해 긴 항속거리를 목표에 두고 설계를 했었는데 이는 무척 성공적이었고 머스탱의 은빛날개가 심볼이 되었다고 한다. 또한 한국공군이 최초로 사용한 전투기이기도하다.
'Engineering' 카테고리의 다른 글
| 진보한 양력모델 Lifting-Surface Method (0) | 2022.10.11 |
|---|---|
| AR비 그리고 Span loading (0) | 2022.10.11 |
| Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유) (0) | 2022.10.07 |
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
