목차
개요
이전 포스팅에서는 AR의 개념과 타원형 양력분포와 일반적 양력분포의 차이와 그 비교에 대해서 알아보았는데 이번 포스팅은 이전 포스팅에 이어서 AR 비가 기체의 양항력에 미치는 영향 그리고 Span loading에 대해서 알아보자.
AR비와 유도항력요소와의 관계
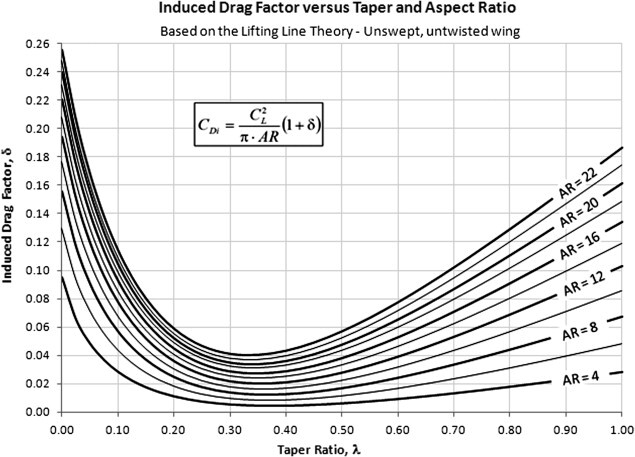
For typical subsonic airplanes, δ ≈ from 0 to 0.16
일반적인 아음속 비행기에서는 Induced Drag factor가 최대 16%의 추가 항력을 만들어낸다.
Primary design factor for minimizing induced drag is not closeness to an elliptical lift distribution, but rather, the ability to make the aspect ratio as large as possible
처음 배웠던 유도항력의 감소를 위한 요소는 타원형의 양력분포에 관련되었던 것(Induced Drag Factor) 인데 결국에는 AR의 변화량이 유도항력계수의 감소에 더 큰 영향을 미친다.
유한 날개에서의 총 양력
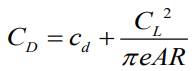
small Cd 는 2차원에서도 있던 항력. viscous + pressure drag
Drag pole 항력곡선 그래프
아래에 보이는 그래프는 항력곡선, 항력극점이라고 불리는 그래프인데 양력계수와 항력계수와의 관계 그래프 이면서 좌측에 위치한 포물선일 수록 AR 비가 커지는 즉 날개가 좌우로 긴 형상의 데이터를 나타내고 있다.
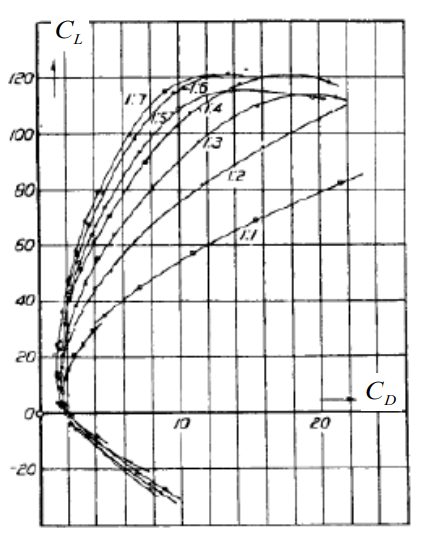
각 데이터는 AR의 차이가 있다.여러 포인트는 받음각 유무. 받음각 상승>양항력계수 상승
동일 양력계수에서 항력계수는 AR이 작아질수록 커짐
동일 항력계수에서 양력계수는 AR이 커질수록 커짐
또한 아래와 같은 식에서 한개의 날개에서의 항력 계수와 AR 비 그리고 다른 날개에서의 AR 비를 알게 되면 다른 날개의 항력계수를 구할수 있게 된다.
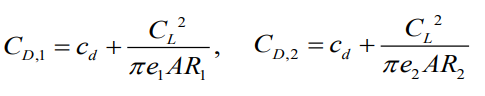
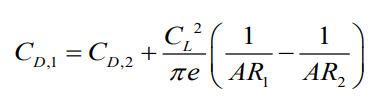
AR1이 AR2보다 큰경우 유도 항력계수가 더 작다
또한 두 AR비를 알고있고 한 케이스에서의 유도 항력계수를 알고있다면 다른 케이스의 유도항력 계수를 추정할 수 있다.
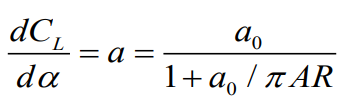
무조건 2차원 날개의 양력계수 기울기보다 작다. 분모 확인
2차원 날개와 유한 날개의 차이점 2가지
- 유도항력이 발생한다.
- Lift slope 가 줄어든다.
기존 2차원 finite wing에서의 Lift slope
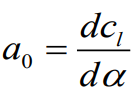
infinite wing에서의 유도받음각이 고려된 Lift slope
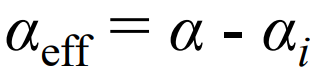
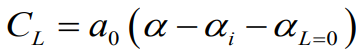
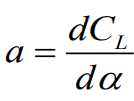
- 유도 받음각이 고려되고 양력분포가 타원형인 Lift slope
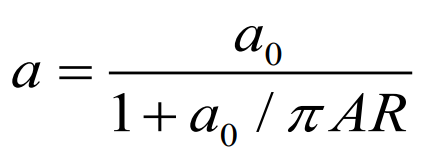
- 유도 받음각이 고려되고 양력분포가 일반적인 Lift slope
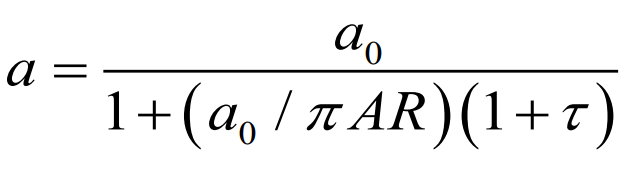
Induced factor 인 τ는 5%~ 25% 의 범위 내에서 존재한다.
AR이 클수록 lift slope이 2차원 wing에서의 lift slope와 가까워진다. 즉 양력효율이 좋아진다.
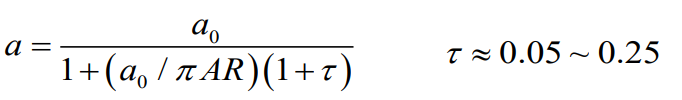
타우 : induced factor for the lift slope : 문제에서는 주어진다.
3차원 양력분포 기울기가 2차원 양력분포 기울기에 가까울 수록 AR 비가 무한대로 간다.
지금까지 AR 비로 양력이 어떻게 변하느니 항력이 감소하니 모든것을 AR비에 대해서 비교를 해보았는데 과연 AR 비가 어떤 비행체의 특성을 보여주는 완벽한 계수일까?
예상했겠지만 아니다. 이다 항공기의 공력해석에 있어서는 수많은 계수가 존재하고 있고 그 중 AR의 상위호환이라고 할 수 있는 Span 길이와 비행체의 무게와의 관계식인 Span Loading 이라는 계수에 대해서 간단히 설명하겠다.
Span Loading
AR비에 대해서 탐구를 할 때는 기껏해야 주위를 흐르고 있는 유체의 속도(자유흐름), 날개의 span 방향의 길이(b), Horse vortex 모델에 따른 양력선 이론 등을 참고 하였는데
실제 비행체의 거동에 대해서 생각해보면 당연한 말이겠지만 지표면 근처가 아닌 때에 따라서 아음속 비행체는 3만 피트 이상을 비행하게 될 것이고 초음속기는 7,8만 피트 이상도 비행하게 될 것이다. 이때 가장 많이 변하는 유체의 특성 중 하나는 기체의 밀도가 될 것이다. 수치적으로도 7만 피트에서의 기체 밀도는 1.225 kg/m3 정도의 지표면에 비해서 0.007 kg/m3 이라는 엄청난 변화를 겪게 되는데
책에 나와있는 예제인 U-2 정찰기가 고도 7만 피트에서 Crusing 상태에 있는 경우의 유도항력값에 대해서 표현해보자.

(크루징 상태에서는 양력과 기체의 무게가 평형을 이루는 고도가 변하지 않는 상태다. 따라서 Lift=Weight)
( ρ∞ = 0.07kg/m3 at 70,000ft)
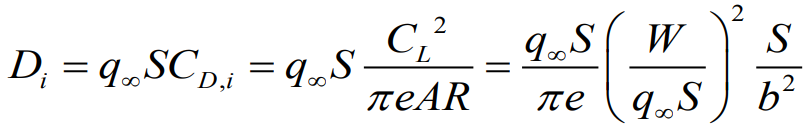
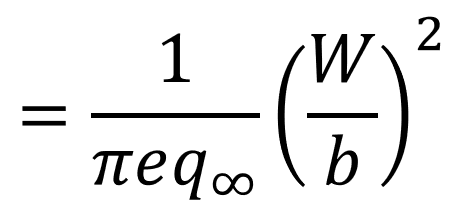

영어 그대로 해석을 해보면 날개 길이당 걸리는 로딩 즉 무게 라는 뜻이다. (크루징 상황이 아니면 달라질 수 있다.)
특수 상황인 Crusing 상황에서는 유도 항력 계수는 Span 길이의 증가에 따라 감소 될 수 있다.
'Engineering' 카테고리의 다른 글
| SpaceX Starship 풀스택 첫 비행시험 17일 오후 9시!--10:13 scrub (0) | 2023.04.17 |
|---|---|
| 진보한 양력모델 Lifting-Surface Method (0) | 2022.10.11 |
| 스핏파이어의 날개 형상이 타원형인 이유 (0) | 2022.10.11 |
| Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유) (0) | 2022.10.07 |
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
목차
개요
이전 포스팅에서는 AR의 개념과 타원형 양력분포와 일반적 양력분포의 차이와 그 비교에 대해서 알아보았는데 이번 포스팅은 이전 포스팅에 이어서 AR 비가 기체의 양항력에 미치는 영향 그리고 Span loading에 대해서 알아보자.
AR비와 유도항력요소와의 관계

For typical subsonic airplanes, δ ≈ from 0 to 0.16
일반적인 아음속 비행기에서는 Induced Drag factor가 최대 16%의 추가 항력을 만들어낸다.
Primary design factor for minimizing induced drag is not closeness to an elliptical lift distribution, but rather, the ability to make the aspect ratio as large as possible
처음 배웠던 유도항력의 감소를 위한 요소는 타원형의 양력분포에 관련되었던 것(Induced Drag Factor) 인데 결국에는 AR의 변화량이 유도항력계수의 감소에 더 큰 영향을 미친다.
유한 날개에서의 총 양력
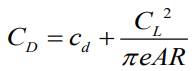
small Cd 는 2차원에서도 있던 항력. viscous + pressure drag
Drag pole 항력곡선 그래프
아래에 보이는 그래프는 항력곡선, 항력극점이라고 불리는 그래프인데 양력계수와 항력계수와의 관계 그래프 이면서 좌측에 위치한 포물선일 수록 AR 비가 커지는 즉 날개가 좌우로 긴 형상의 데이터를 나타내고 있다.

각 데이터는 AR의 차이가 있다.여러 포인트는 받음각 유무. 받음각 상승>양항력계수 상승
동일 양력계수에서 항력계수는 AR이 작아질수록 커짐
동일 항력계수에서 양력계수는 AR이 커질수록 커짐
또한 아래와 같은 식에서 한개의 날개에서의 항력 계수와 AR 비 그리고 다른 날개에서의 AR 비를 알게 되면 다른 날개의 항력계수를 구할수 있게 된다.
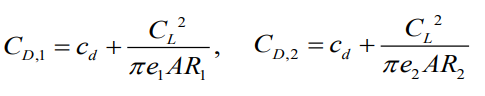
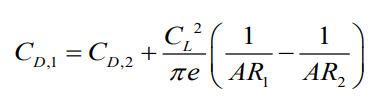
AR1이 AR2보다 큰경우 유도 항력계수가 더 작다
또한 두 AR비를 알고있고 한 케이스에서의 유도 항력계수를 알고있다면 다른 케이스의 유도항력 계수를 추정할 수 있다.
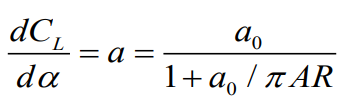
무조건 2차원 날개의 양력계수 기울기보다 작다. 분모 확인
2차원 날개와 유한 날개의 차이점 2가지
- 유도항력이 발생한다.
- Lift slope 가 줄어든다.
기존 2차원 finite wing에서의 Lift slope
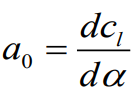
infinite wing에서의 유도받음각이 고려된 Lift slope
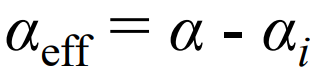
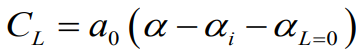
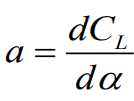
- 유도 받음각이 고려되고 양력분포가 타원형인 Lift slope
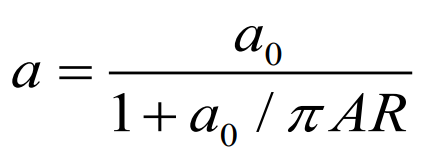
- 유도 받음각이 고려되고 양력분포가 일반적인 Lift slope
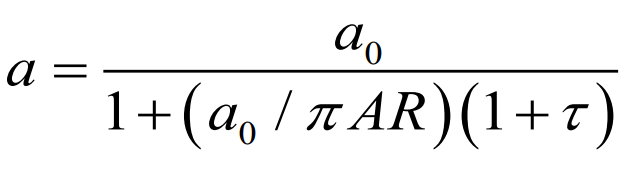
Induced factor 인 τ는 5%~ 25% 의 범위 내에서 존재한다.
AR이 클수록 lift slope이 2차원 wing에서의 lift slope와 가까워진다. 즉 양력효율이 좋아진다.
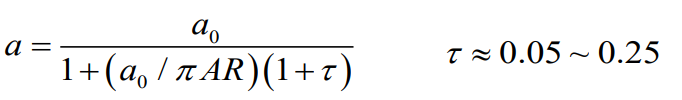
타우 : induced factor for the lift slope : 문제에서는 주어진다.
3차원 양력분포 기울기가 2차원 양력분포 기울기에 가까울 수록 AR 비가 무한대로 간다.
지금까지 AR 비로 양력이 어떻게 변하느니 항력이 감소하니 모든것을 AR비에 대해서 비교를 해보았는데 과연 AR 비가 어떤 비행체의 특성을 보여주는 완벽한 계수일까?
예상했겠지만 아니다. 이다 항공기의 공력해석에 있어서는 수많은 계수가 존재하고 있고 그 중 AR의 상위호환이라고 할 수 있는 Span 길이와 비행체의 무게와의 관계식인 Span Loading 이라는 계수에 대해서 간단히 설명하겠다.
Span Loading
AR비에 대해서 탐구를 할 때는 기껏해야 주위를 흐르고 있는 유체의 속도(자유흐름), 날개의 span 방향의 길이(b), Horse vortex 모델에 따른 양력선 이론 등을 참고 하였는데
실제 비행체의 거동에 대해서 생각해보면 당연한 말이겠지만 지표면 근처가 아닌 때에 따라서 아음속 비행체는 3만 피트 이상을 비행하게 될 것이고 초음속기는 7,8만 피트 이상도 비행하게 될 것이다. 이때 가장 많이 변하는 유체의 특성 중 하나는 기체의 밀도가 될 것이다. 수치적으로도 7만 피트에서의 기체 밀도는 1.225 kg/m3 정도의 지표면에 비해서 0.007 kg/m3 이라는 엄청난 변화를 겪게 되는데
책에 나와있는 예제인 U-2 정찰기가 고도 7만 피트에서 Crusing 상태에 있는 경우의 유도항력값에 대해서 표현해보자.

(크루징 상태에서는 양력과 기체의 무게가 평형을 이루는 고도가 변하지 않는 상태다. 따라서 Lift=Weight)
( ρ∞ = 0.07kg/m3 at 70,000ft)
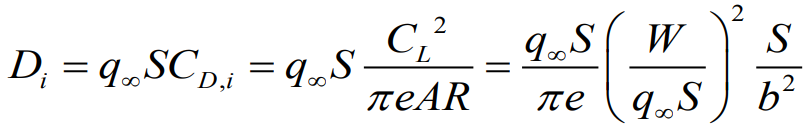
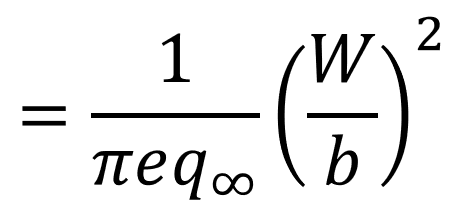

영어 그대로 해석을 해보면 날개 길이당 걸리는 로딩 즉 무게 라는 뜻이다. (크루징 상황이 아니면 달라질 수 있다.)
특수 상황인 Crusing 상황에서는 유도 항력 계수는 Span 길이의 증가에 따라 감소 될 수 있다.
'Engineering' 카테고리의 다른 글
| SpaceX Starship 풀스택 첫 비행시험 17일 오후 9시!--10:13 scrub (0) | 2023.04.17 |
|---|---|
| 진보한 양력모델 Lifting-Surface Method (0) | 2022.10.11 |
| 스핏파이어의 날개 형상이 타원형인 이유 (0) | 2022.10.11 |
| Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유) (0) | 2022.10.07 |
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
