Vortex Filament, Circulration, Horseshoe Vortex(Bound vortex+ Free trailing vortex), Biot-Savart 정리 들을 통해 Prandtl's Classical Lifting Line을 설명해주는 포스팅
와류 필라멘트, 회전, 말발굽 와류(경계 와류+ 자유 흐름 와류), 비오 사바르 정리 들을 통해 프란틀의 양력선 이론을 설명해주는 포스팅
목차
개요
이전 포스팅에서는 Downwash 와 Vortex가 Mainwing에 작용하는 힘 등을 대략적으로 알아보았는데 이번 포스팅에서는
이러한 유체의 거동을
Vortex Filament와 Circulration의 개념을 기반으로
주익의 주변 유체 거동을 Horseshoe Vortex(Bound + Free trailing) 형태로 표현을 하되
Biot-Savart 정리를 만족시켜 해석의 단순화에 대한 정당함을 부여한
Prandtl's Classical Lifting Line 정리에 대해서 알아볼것이다.
그리고 그 다음 포스팅에서는
Prandtl's Classical Lifting Line 의 한계점에 대해 알아보고 이를 Trailling Vortex Sheet 개념을 적용시켜 모순을 해결하여
흔히 알고있는 Prandtl's Lifting-Line 정리가 어떻게 도출되는지도 설명해보겠다.
Vortex filament, circulation 의 정의
Vortex filament
: line whose tangent is everywhere parallel to the local vorticity vector.
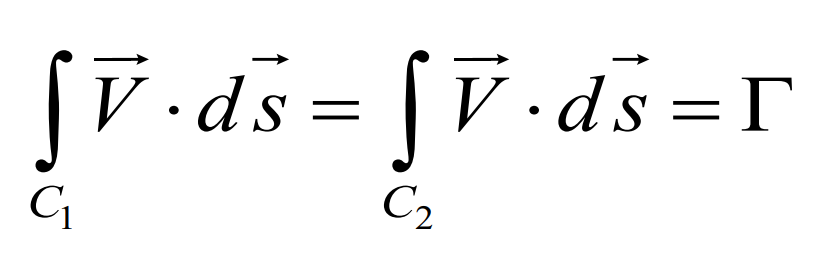
연속체 역학에 있어서 존재하는 와도에 평행하는 선과 항상 수직인 선을 뜻하는데 설명은 어렵지만 아래 그림에서 보면

사진의 소용돌이 (와류)의 각 지점에서의 벡터성분과 평행한 선에 항상 수직인 선 = 소용돌이의 중심선
이라고 이해를 하면 쉬울수 있다.
특성으로는
- 당연히 직선으로만 생성되는것이 아니라 휘어질수도 있다.
- 한 방향으로 무한하게 뻗어나가야 한다.
Circulation
:the path integral of the fluid velocity around a closed curve in a fluid flow
닫힌 곡선의 유체의 성분이라고 보면된다. 정지해 있으면 flow 가 아니기 때문에 움직이고 있는데 움직인다면 시계나 반시계 어느쪽이로던지 움직여야될테고 우리는 이것을 유체의 circulation 이라고 부른다.
위의 사진에 보면 vortex filament의 주위로 유체가 회전을 하고 있지 않은가?
The circulation is taken about any path enclosing the filament
같이 생각해보면 filament를 감싸고 있는 circulation 이라고 이해할 수 있고
이러한 회전에 의해 유도되는 vortex filament의 강도는
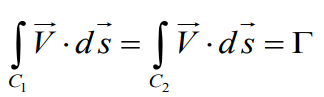
이렇게 표현된다. Γ = 유체의 circulation 정도, filament의 강도
Biot-Savart Law
전자기학을 고등학교때 잘 이해했다면 이것이 전류에 의해 발생된 자기장을 구하는 것과 비슷해서 이해가 잘 될테고 그렇지 않다면

발생한 소용돌이가 어느 일정 수준까지만 도달하고 갑자기 사라지는지 발생한 소용돌이 중심에서 점점 멀어질 수록 강도가 약해져가면서 그 힘이 0이 될때까지 퍼져가는지 생각해보면 쉽다.
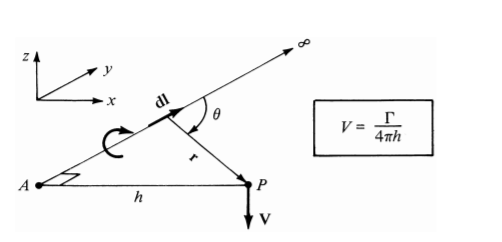
이 공식은 위에서 소용돌이를 하나의 직선으로 간단하게 표현한 식을 이용해 거리별 특정 지점에서의 속도 성분(힘과 방향)을 구하는 식을 알아 볼 것이다.
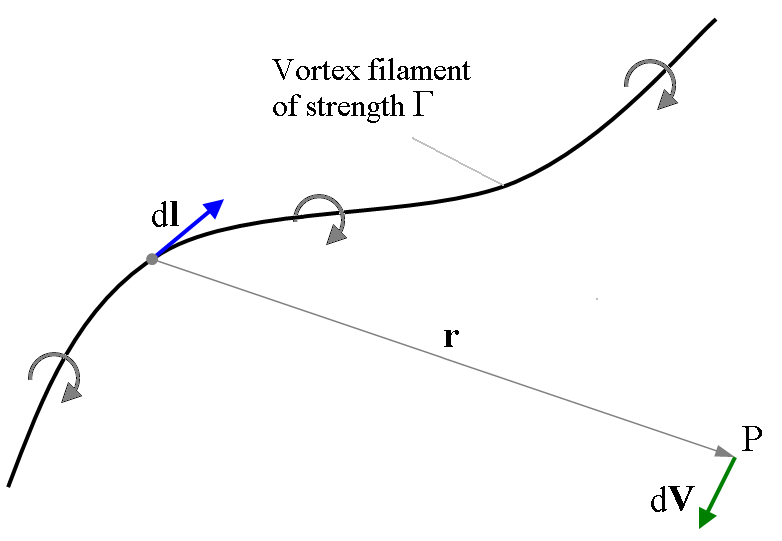
간략하게 필라멘트 위에 있는 dl 성분과 r 만큼 떨어진 P지점에서의 속도 성분인 dV 를 구해내는 식이다.
The velocity induced at P
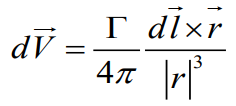
식으로 나타내면 이렇게 나타낼 수 있다.
이러한 식에서 특수한 상황 두가지를 상정해서
1. 직선이고 길이가 무한인 경우 ( Straight Vortex Filament of Infinite Length )
2. 직선이고 길이가 한쪽으로 무한한 경우( Straight Vortex Filament of Semi-infinite)
위에 대한 속도 성분을 생각해보면 직선이기 때문에 방향 성분은 일정한 규칙을 가지게 되고 속도의 크기 성분에 대해서 구해보자면
1. 직선이고 길이가 무한인 경우 ( Straight Vortex Filament of Infinite Length )
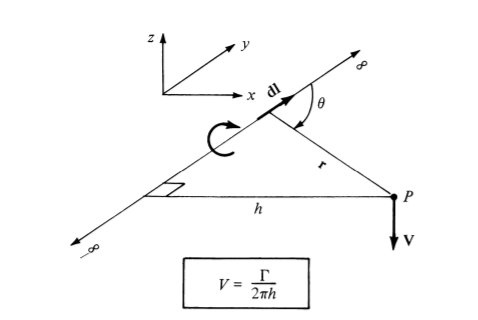
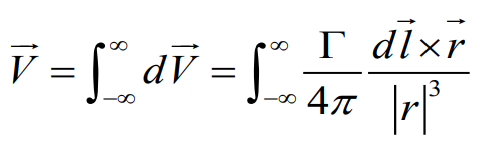
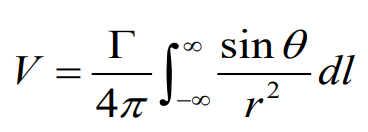
h가 수직하다는 특성을 이해하여 추가적으로 식을 세워주게되면
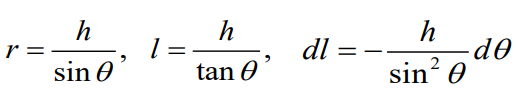
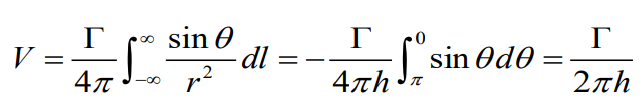
위와 같은 계산 결과가 나온다.
2. 직선이고 길이가 한쪽으로 무한한 경우( Straight Vortex Filament of Semi-infinite)
1번에서 했던 계산과 구간만 다르게 해서 식을 세워주면
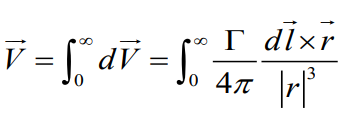
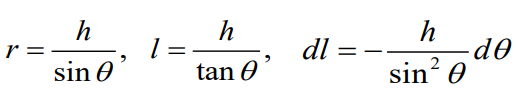
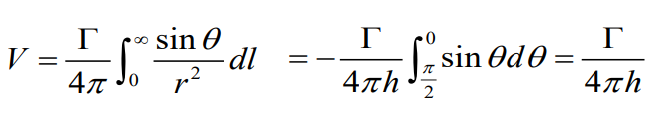
직관적으로 생각했을때에도 vortex의 구간이 반으로 줄었으니 속도의 강도도 반으로 줄어야하지 않겠는가?
정리해보자면 Inf와 semi-Inf 각각의 경우에 임의의 점 P에 유도되는 속도는

이렇게 정리 할 수 있다.
다음으로는 이러한 3차원 장에서의 유도 성분들을 통해 단순화를 하기위한 조건들을 알아보겠다.
Helmholtz's Theorem 에서의 조건
모든 벡터장은 스칼라 포텐셜 V와 벡터 포텐셜 A로 나타낼수 있다. 라고 설명을 많이 하는 정리이다.
이 정리의 조건으로는 벡터의 발산과 회전이 하나로 정의되고 닫힌 표면적의 경계 조건이 정해지면 이라는 조건이 존재하는데
어렵게 생각하지말고 우리가 위에서 했던 것들을 생각해보자.
소용돌이(벡터로 이루어진 장)을 스칼라 포텐셜(속도의 강도)와 벡터 포텐셜(속도의 주위에 있는 와류들)로 나타냈다.
벡터장의 간소화를 하기 위한 양력선 이론을 이해하기 위해서 중요하게 보아야되는 조건은 아래와 같다.
1. The strength of a vortex filament is constant along its length
vortex filament의 강도가 모든 길이마다 일정해야한다.
= 스칼라 포텐셜 V는 하나로 정의되어야한다.
2. A vortex filament cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path
vortex filament는 유체 안에서 끝나면 안된다. 닫힌 경계면까지의 경계 연장이 이어져야 한다.
= 닫힌 표면적의 경계조건이 만족되야 한다. 오늘 다룰 모델에서는 유동 내 날개의 벡터장에 대해서 사용할 텐데 이때 filament가 유동 내에서 끝이 나면 안되기 때문에 infinite 하게 이어져야한다.
Lift Distribution Along the span 날개 위 양력 분포
유한한 길이의 날개 위에서 양력에 영향을 줄 만한 요소가 무엇이 있을까?? = 양력 분배 요소

간단하게부터 위의 사진을 보면서 생각해보자면
- 각 부분 마다 날개의 단면 길이가 다를수 있다.
- 날개 단면의 두께가 달라보일수 있다.
라고 생각 할수 있겠다. 여기서 좀 더 전공지식을 넣어보자면
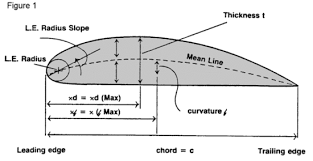
위에 보이는 에어포일의 형상마다 만들어지는 양력의 정도도 달라지고 받음각 또한 달라진다.
- chord
- Geometric Angle of Attack
- 같은 날개 내에 있더라도 동일한 받음각에서 생성하는 양력이 다르게 설계되어있다.
예시를 들어서 이해를 돕자면
1. Chord 길이가 어디던지 같은 날개의 경우

감이 좀 잡히는가? 김밥처럼 어딜 썰어서 비교해도 다 동등한 모양이 나올 것이다.
하지만 이러한 직사각형 모양의 날개는 흔하지 않은 편이다. 따라서 구간 별로 다른 chord 를 가진 익형을 수식으로 나타내보면 이렇게 나타낼 수 있다.
2. Geometric AOA(angle of attack) 다른 경우
1) 비행기가 설계될 당시에 안쪽의 날개가 부착 되어있는 AOA 와 날개 끝의 AOA 가 다르다.
2) 각 부분의 에어포일 형상이 다른 두개 이상이 같이 존재한다.
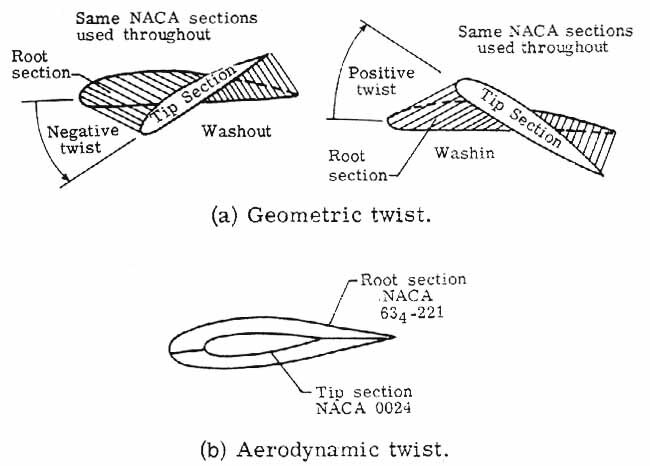
1번의 경우 Geometric twist 라고 하는데
동일한 성분을 가진 에어포일을 사용해도 스크류바처럼 살짝 꼬여있게 되는 형상을 가지고 있는 경우도 있다.
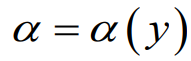
2번의 경우 Aerodynamic twist 라고 하는데
항공기의 효율을 계산하여 예로들어 root 부분의 성질과 tip 부분의 성질 각각에 효율적인 에어포일을 배치하는 것처럼 서로 다른 형상의 에어포일이 구간별로 배치 되어있음을 말한다.
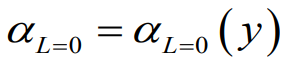
따라서 위와 같은 3가지의 다양함으로 인해서 날개에서 발생하는 양력의 분배는 구간별로 다르게 도출된다. 가 결론이다.
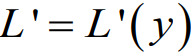
( ') 프라임이 붙은 경우는 단위 길이당 양력을 나타낸다.
또한 Kutta-Joukowski 정리에 따르면 Circulation 도 아래와 같이 나타낼수 있다.
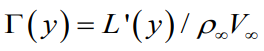
그럼 지금까지 배웠던 개념들을 잘 숙지한 이후에 본격적으로 양력선 이론 (날개 위에 형성되는 양력들의 분포 정도를 알아내기 위한 이론)을 살펴보자
또한 유체 내에서 압력의 분포도 연속적임을 게속 생각하고 있어야한다 쉽게 말하자면 위 아래 날개의 압력차가 존재하는데 날개를 기준으로 갑자기 양력이 커지거나 작아지는 것이 아니라 그 변화가 연속적으로 이루어 진다는 것이다. 이를 대입해서 생각해보면 날개 끝에서는 윗날개와 아랫날개의 압력차가 0이어야 한다.
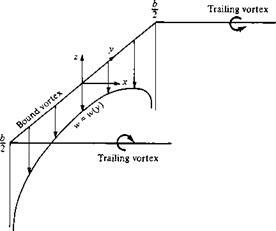
Prandltl`s Classical Lifting Line Therory (Horseshoe Vortex)
이제부터 실제 날개를 간단하게 모델링 하는 과정이라고 볼 수 있는데
양력이 생성되는 날개를 Kutta-Joukoski 이론을 이용해서(포스팅예정) 날개의 앞부분으로 오는 Freesteam(유체의 흐름)에 수직한 span 방향의 선을 하나 임의로 그려서 적용시켜준다.
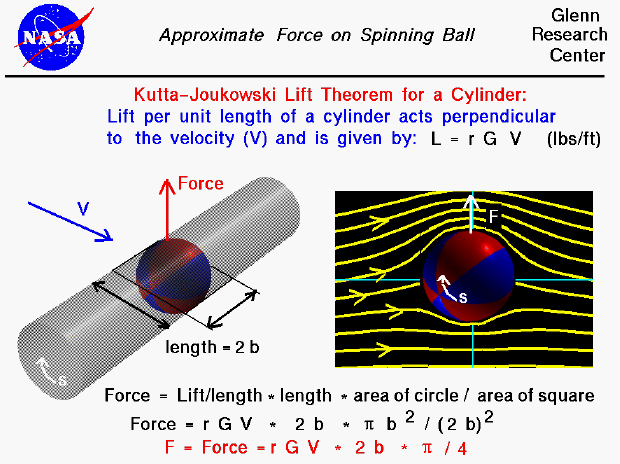
자유류와 Circulation이 수직한 경우에 Force 가 발생한다.
위는 면적이 존재하는 원통의 경우지만 양력선 이론에서는 면적이 존재하지 않는 선으로만 진행을 한다.
Bounded vortex 의 Circulation 과 자유류의 방향이 아랫 그림에서 보게되면 수직하기 때문에 위로 올라가는 Lift 가 발생하게 된다.
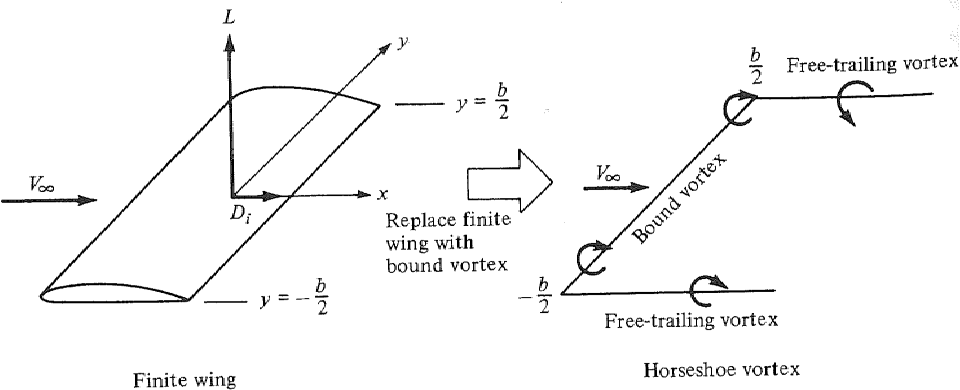
좌우에 보면 Free- Trailing vortex 가 있게 되는데 이를 넣은 이유는
Helmholtz`s theorem 에 있던 조건 중 하나인 vortex filament cannot end in the fluid 조건을 만족 시키기 위해서 추가를 한 것인데 Kutta 이론을 살펴보았을때
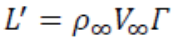
Vinf(자유류 ; 비행기가 날아갈때 앞에서 불어오는 바람)이 free-trailing vortex에서는 align 되어 (같은 방향) 있으므로 양력 형성을 하지 못한다. 자유류와 circulation이 perpendicular 하지 않기 때문에 힘에 추가적인 영향을 주지 않는다.
따라서 이를 추가해주게 되면 헬름 홀츠 정리를 만족시켜서 벡터장의 단순화를 할 수있다는 장점이 있지만 최종 모델에 대해서는 추가적으로 힘을 가해주는 것이 없기 때문에 단순화를 위한 추가라고 볼 수있다.
이러한 두개의 free-trailing vortex와 하나의 bounded vortex로 이루어져 있는 vortex를 말발굽을 닮았다고 하여 Horseshoe vortex 라고 불린다.
따라서 이러한 말발굽 와류 모델 중 Bounded vortex가 날개에 표현하는 힘은
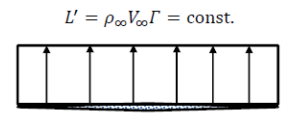
모든 지점에서 동등한 양의 단위 길이당 양력을 나타내고 있다.
그럼 양옆의 Free-trailing vortex는 아무일도 하지 않고 있을까? 쿱타 이론에 의해 양력을 생성하고 있지 않은 것일뿐이지 날개에 아무 영향도 주고있지 않은 것은 아니다. 형성한 모델을 위에서 바라보면
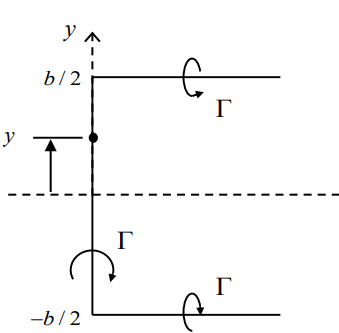
Helmhotz 의 조건에 의해서 이어져있는 vortex filament는 다 같은 강도를 가지고 있고 Biot-Savart law의 semi-infinite straight 이론을 이용하여 bounded vortex로 나타낸 main wing에 걸리는 down wash (w)를 구해낼수 있다.
downwash애 대해 알고싶다면
내리흐름 Downwash & 유도항력 Induced drag
새들이 V자로 나는 이유 (전공 지식을 곁들인) 그리고 이를 이해하기 위한 여러 설명들 목차 개요 유한 날개에서의 공기역학적 특성을 알아보자. 베르누이 정리 마그누스 효과 d'Alembert Paradox Kutta
nstgic3.tistory.com
Biot-Savart law에 따르면
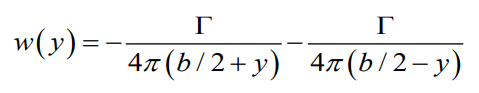
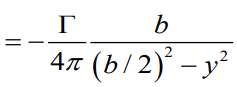
양옆의 free-trailing vortex가 wing에 가해지는 downwash magnitude를 구할수 있게 된다.
구해진 downwash 를 3D형상의 그래프로 나타내보면
이러한 양력 분포가 발생하는 것을 확인 할 수 있는데
여기서 수식을 살펴보게 되면 모순이 발생한다.
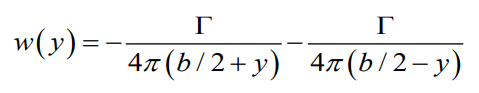
만약 날개의 tip 을 측정하려고 y에 b/2 나 -b/2 를 집어넣게 되면 downwash 의 값은 무한대로 발산하게 된다.
이러한 모순점을 해결하기 위해서는 이러한 Horseshoe를 무한하게 겹치는 Superosition 방식을 사용하게 되는데
이는 다음 포스팅에서 자세히 다뤄보도록하겠다.
'Engineering' 카테고리의 다른 글
| Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유) (0) | 2022.10.07 |
|---|---|
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
Vortex Filament, Circulration, Horseshoe Vortex(Bound vortex+ Free trailing vortex), Biot-Savart 정리 들을 통해 Prandtl's Classical Lifting Line을 설명해주는 포스팅
와류 필라멘트, 회전, 말발굽 와류(경계 와류+ 자유 흐름 와류), 비오 사바르 정리 들을 통해 프란틀의 양력선 이론을 설명해주는 포스팅
목차
개요
이전 포스팅에서는 Downwash 와 Vortex가 Mainwing에 작용하는 힘 등을 대략적으로 알아보았는데 이번 포스팅에서는
이러한 유체의 거동을
Vortex Filament와 Circulration의 개념을 기반으로
주익의 주변 유체 거동을 Horseshoe Vortex(Bound + Free trailing) 형태로 표현을 하되
Biot-Savart 정리를 만족시켜 해석의 단순화에 대한 정당함을 부여한
Prandtl's Classical Lifting Line 정리에 대해서 알아볼것이다.
그리고 그 다음 포스팅에서는
Prandtl's Classical Lifting Line 의 한계점에 대해 알아보고 이를 Trailling Vortex Sheet 개념을 적용시켜 모순을 해결하여
흔히 알고있는 Prandtl's Lifting-Line 정리가 어떻게 도출되는지도 설명해보겠다.
Vortex filament, circulation 의 정의
Vortex filament
: line whose tangent is everywhere parallel to the local vorticity vector.
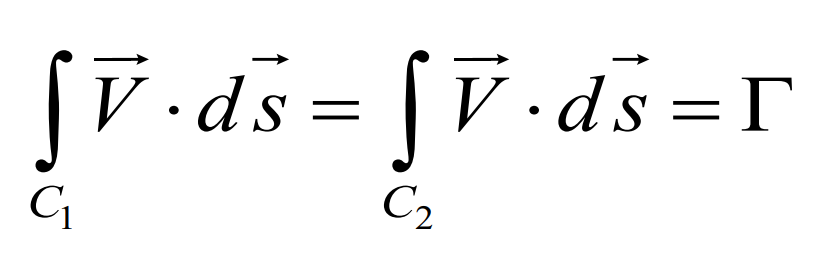
연속체 역학에 있어서 존재하는 와도에 평행하는 선과 항상 수직인 선을 뜻하는데 설명은 어렵지만 아래 그림에서 보면

사진의 소용돌이 (와류)의 각 지점에서의 벡터성분과 평행한 선에 항상 수직인 선 = 소용돌이의 중심선
이라고 이해를 하면 쉬울수 있다.
특성으로는
- 당연히 직선으로만 생성되는것이 아니라 휘어질수도 있다.
- 한 방향으로 무한하게 뻗어나가야 한다.
Circulation
:the path integral of the fluid velocity around a closed curve in a fluid flow
닫힌 곡선의 유체의 성분이라고 보면된다. 정지해 있으면 flow 가 아니기 때문에 움직이고 있는데 움직인다면 시계나 반시계 어느쪽이로던지 움직여야될테고 우리는 이것을 유체의 circulation 이라고 부른다.
위의 사진에 보면 vortex filament의 주위로 유체가 회전을 하고 있지 않은가?
The circulation is taken about any path enclosing the filament
같이 생각해보면 filament를 감싸고 있는 circulation 이라고 이해할 수 있고
이러한 회전에 의해 유도되는 vortex filament의 강도는
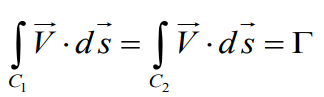
이렇게 표현된다. Γ = 유체의 circulation 정도, filament의 강도
Biot-Savart Law
전자기학을 고등학교때 잘 이해했다면 이것이 전류에 의해 발생된 자기장을 구하는 것과 비슷해서 이해가 잘 될테고 그렇지 않다면

발생한 소용돌이가 어느 일정 수준까지만 도달하고 갑자기 사라지는지 발생한 소용돌이 중심에서 점점 멀어질 수록 강도가 약해져가면서 그 힘이 0이 될때까지 퍼져가는지 생각해보면 쉽다.
이 공식은 위에서 소용돌이를 하나의 직선으로 간단하게 표현한 식을 이용해 거리별 특정 지점에서의 속도 성분(힘과 방향)을 구하는 식을 알아 볼 것이다.

간략하게 필라멘트 위에 있는 dl 성분과 r 만큼 떨어진 P지점에서의 속도 성분인 dV 를 구해내는 식이다.
The velocity induced at P
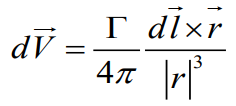
식으로 나타내면 이렇게 나타낼 수 있다.
이러한 식에서 특수한 상황 두가지를 상정해서
1. 직선이고 길이가 무한인 경우 ( Straight Vortex Filament of Infinite Length )
2. 직선이고 길이가 한쪽으로 무한한 경우( Straight Vortex Filament of Semi-infinite)
위에 대한 속도 성분을 생각해보면 직선이기 때문에 방향 성분은 일정한 규칙을 가지게 되고 속도의 크기 성분에 대해서 구해보자면
1. 직선이고 길이가 무한인 경우 ( Straight Vortex Filament of Infinite Length )

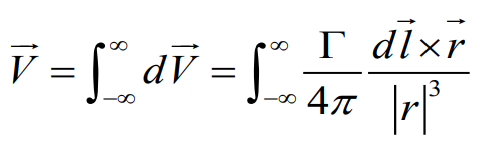
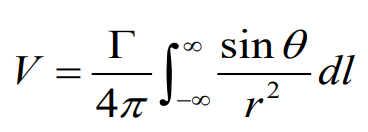
h가 수직하다는 특성을 이해하여 추가적으로 식을 세워주게되면
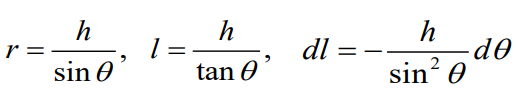
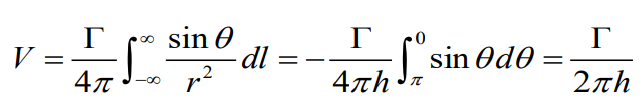
위와 같은 계산 결과가 나온다.
2. 직선이고 길이가 한쪽으로 무한한 경우( Straight Vortex Filament of Semi-infinite)

1번에서 했던 계산과 구간만 다르게 해서 식을 세워주면
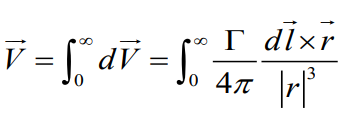
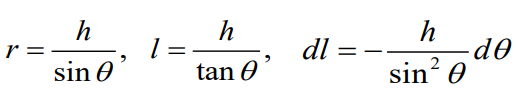
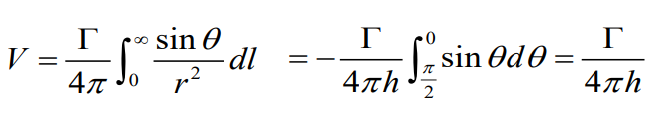
직관적으로 생각했을때에도 vortex의 구간이 반으로 줄었으니 속도의 강도도 반으로 줄어야하지 않겠는가?
정리해보자면 Inf와 semi-Inf 각각의 경우에 임의의 점 P에 유도되는 속도는

이렇게 정리 할 수 있다.
다음으로는 이러한 3차원 장에서의 유도 성분들을 통해 단순화를 하기위한 조건들을 알아보겠다.
Helmholtz's Theorem 에서의 조건
모든 벡터장은 스칼라 포텐셜 V와 벡터 포텐셜 A로 나타낼수 있다. 라고 설명을 많이 하는 정리이다.
이 정리의 조건으로는 벡터의 발산과 회전이 하나로 정의되고 닫힌 표면적의 경계 조건이 정해지면 이라는 조건이 존재하는데
어렵게 생각하지말고 우리가 위에서 했던 것들을 생각해보자.
소용돌이(벡터로 이루어진 장)을 스칼라 포텐셜(속도의 강도)와 벡터 포텐셜(속도의 주위에 있는 와류들)로 나타냈다.
벡터장의 간소화를 하기 위한 양력선 이론을 이해하기 위해서 중요하게 보아야되는 조건은 아래와 같다.
1. The strength of a vortex filament is constant along its length
vortex filament의 강도가 모든 길이마다 일정해야한다.
= 스칼라 포텐셜 V는 하나로 정의되어야한다.
2. A vortex filament cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path
vortex filament는 유체 안에서 끝나면 안된다. 닫힌 경계면까지의 경계 연장이 이어져야 한다.
= 닫힌 표면적의 경계조건이 만족되야 한다. 오늘 다룰 모델에서는 유동 내 날개의 벡터장에 대해서 사용할 텐데 이때 filament가 유동 내에서 끝이 나면 안되기 때문에 infinite 하게 이어져야한다.
Lift Distribution Along the span 날개 위 양력 분포
유한한 길이의 날개 위에서 양력에 영향을 줄 만한 요소가 무엇이 있을까?? = 양력 분배 요소

간단하게부터 위의 사진을 보면서 생각해보자면
- 각 부분 마다 날개의 단면 길이가 다를수 있다.
- 날개 단면의 두께가 달라보일수 있다.
라고 생각 할수 있겠다. 여기서 좀 더 전공지식을 넣어보자면

위에 보이는 에어포일의 형상마다 만들어지는 양력의 정도도 달라지고 받음각 또한 달라진다.
- chord
- Geometric Angle of Attack
- 같은 날개 내에 있더라도 동일한 받음각에서 생성하는 양력이 다르게 설계되어있다.
예시를 들어서 이해를 돕자면
1. Chord 길이가 어디던지 같은 날개의 경우

감이 좀 잡히는가? 김밥처럼 어딜 썰어서 비교해도 다 동등한 모양이 나올 것이다.
하지만 이러한 직사각형 모양의 날개는 흔하지 않은 편이다. 따라서 구간 별로 다른 chord 를 가진 익형을 수식으로 나타내보면 이렇게 나타낼 수 있다.
2. Geometric AOA(angle of attack) 다른 경우
1) 비행기가 설계될 당시에 안쪽의 날개가 부착 되어있는 AOA 와 날개 끝의 AOA 가 다르다.
2) 각 부분의 에어포일 형상이 다른 두개 이상이 같이 존재한다.

1번의 경우 Geometric twist 라고 하는데
동일한 성분을 가진 에어포일을 사용해도 스크류바처럼 살짝 꼬여있게 되는 형상을 가지고 있는 경우도 있다.
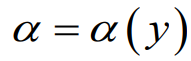
2번의 경우 Aerodynamic twist 라고 하는데
항공기의 효율을 계산하여 예로들어 root 부분의 성질과 tip 부분의 성질 각각에 효율적인 에어포일을 배치하는 것처럼 서로 다른 형상의 에어포일이 구간별로 배치 되어있음을 말한다.
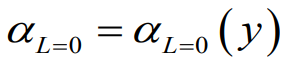
따라서 위와 같은 3가지의 다양함으로 인해서 날개에서 발생하는 양력의 분배는 구간별로 다르게 도출된다. 가 결론이다.
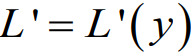
( ') 프라임이 붙은 경우는 단위 길이당 양력을 나타낸다.
또한 Kutta-Joukowski 정리에 따르면 Circulation 도 아래와 같이 나타낼수 있다.
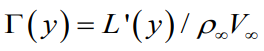
그럼 지금까지 배웠던 개념들을 잘 숙지한 이후에 본격적으로 양력선 이론 (날개 위에 형성되는 양력들의 분포 정도를 알아내기 위한 이론)을 살펴보자
또한 유체 내에서 압력의 분포도 연속적임을 게속 생각하고 있어야한다 쉽게 말하자면 위 아래 날개의 압력차가 존재하는데 날개를 기준으로 갑자기 양력이 커지거나 작아지는 것이 아니라 그 변화가 연속적으로 이루어 진다는 것이다. 이를 대입해서 생각해보면 날개 끝에서는 윗날개와 아랫날개의 압력차가 0이어야 한다.
Prandltl`s Classical Lifting Line Therory (Horseshoe Vortex)
이제부터 실제 날개를 간단하게 모델링 하는 과정이라고 볼 수 있는데
양력이 생성되는 날개를 Kutta-Joukoski 이론을 이용해서(포스팅예정) 날개의 앞부분으로 오는 Freesteam(유체의 흐름)에 수직한 span 방향의 선을 하나 임의로 그려서 적용시켜준다.

자유류와 Circulation이 수직한 경우에 Force 가 발생한다.
위는 면적이 존재하는 원통의 경우지만 양력선 이론에서는 면적이 존재하지 않는 선으로만 진행을 한다.
Bounded vortex 의 Circulation 과 자유류의 방향이 아랫 그림에서 보게되면 수직하기 때문에 위로 올라가는 Lift 가 발생하게 된다.

좌우에 보면 Free- Trailing vortex 가 있게 되는데 이를 넣은 이유는
Helmholtz`s theorem 에 있던 조건 중 하나인 vortex filament cannot end in the fluid 조건을 만족 시키기 위해서 추가를 한 것인데 Kutta 이론을 살펴보았을때
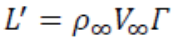
Vinf(자유류 ; 비행기가 날아갈때 앞에서 불어오는 바람)이 free-trailing vortex에서는 align 되어 (같은 방향) 있으므로 양력 형성을 하지 못한다. 자유류와 circulation이 perpendicular 하지 않기 때문에 힘에 추가적인 영향을 주지 않는다.
따라서 이를 추가해주게 되면 헬름 홀츠 정리를 만족시켜서 벡터장의 단순화를 할 수있다는 장점이 있지만 최종 모델에 대해서는 추가적으로 힘을 가해주는 것이 없기 때문에 단순화를 위한 추가라고 볼 수있다.
이러한 두개의 free-trailing vortex와 하나의 bounded vortex로 이루어져 있는 vortex를 말발굽을 닮았다고 하여 Horseshoe vortex 라고 불린다.
따라서 이러한 말발굽 와류 모델 중 Bounded vortex가 날개에 표현하는 힘은

모든 지점에서 동등한 양의 단위 길이당 양력을 나타내고 있다.
그럼 양옆의 Free-trailing vortex는 아무일도 하지 않고 있을까? 쿱타 이론에 의해 양력을 생성하고 있지 않은 것일뿐이지 날개에 아무 영향도 주고있지 않은 것은 아니다. 형성한 모델을 위에서 바라보면

Helmhotz 의 조건에 의해서 이어져있는 vortex filament는 다 같은 강도를 가지고 있고 Biot-Savart law의 semi-infinite straight 이론을 이용하여 bounded vortex로 나타낸 main wing에 걸리는 down wash (w)를 구해낼수 있다.
downwash애 대해 알고싶다면
내리흐름 Downwash & 유도항력 Induced drag
새들이 V자로 나는 이유 (전공 지식을 곁들인) 그리고 이를 이해하기 위한 여러 설명들 목차 개요 유한 날개에서의 공기역학적 특성을 알아보자. 베르누이 정리 마그누스 효과 d'Alembert Paradox Kutta
nstgic3.tistory.com
Biot-Savart law에 따르면
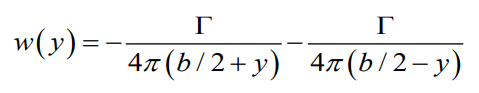
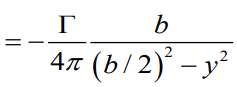
양옆의 free-trailing vortex가 wing에 가해지는 downwash magnitude를 구할수 있게 된다.
구해진 downwash 를 3D형상의 그래프로 나타내보면

이러한 양력 분포가 발생하는 것을 확인 할 수 있는데
여기서 수식을 살펴보게 되면 모순이 발생한다.
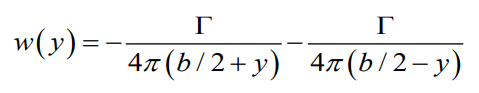
만약 날개의 tip 을 측정하려고 y에 b/2 나 -b/2 를 집어넣게 되면 downwash 의 값은 무한대로 발산하게 된다.
이러한 모순점을 해결하기 위해서는 이러한 Horseshoe를 무한하게 겹치는 Superosition 방식을 사용하게 되는데
이는 다음 포스팅에서 자세히 다뤄보도록하겠다.
'Engineering' 카테고리의 다른 글
| Elliptical Lift distribution 타원형 양력분포와 AR (부제: 글라이더가 날개가 긴 이유) (0) | 2022.10.07 |
|---|---|
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
| Initial/Final value theorem 라플라스 변환 초기값,최종값 정리 (0) | 2022.09.27 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
