목차
개요
이전 시간에 라플라스의 개념과 성립 조건, 특성들을 배웠는데 이어서 최종값과 최초값 정리를 알아보자.
Laplace Transformation 라플라스 변환
목차 개요 Linear ordinary differential equation(선형 상미분방정식)의 해를 구하는 방식으로 많이 쓰인다. 어렵게 생각하지말고 수학자들이 만든 해를 쉽게 구하는 방식이라고 보면 된다.(수학적으로 유
nstgic3.tistory.com
둘다 라플라스 변환의 미분식에서 유도가 되며 이전 내용에 대한 충분한 이해가 있어야한다.
초기값 정리
두가지 방법으로 초기값 정리를 증명 해낼 수 있는데 (사실 순서만 좀 다를뿐이다.)
둘다 라플라스 변환 + 0에서의 불연속성을 고려한 디랙 델타 함수를 이용한 변형식에서 시작된다는 사실은 같다.
1. 1차 도함수의 라플라스 변환에서 시작
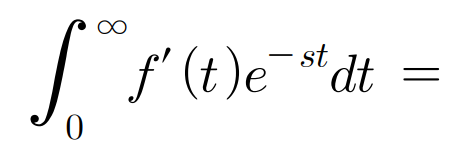
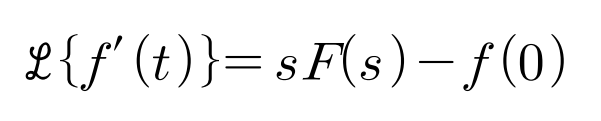
0에서 불연속한 경우에 0- 로 시작하는 함수로 고려해야지 t=0에서의 불연속점이 존재하였을때 수학적으로 성립함을 보여줄 수 있기 때문에 (단위 계단 함수의 성질)
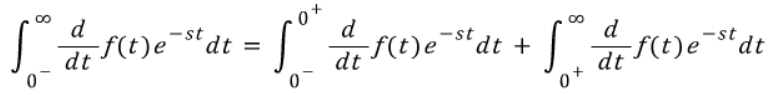
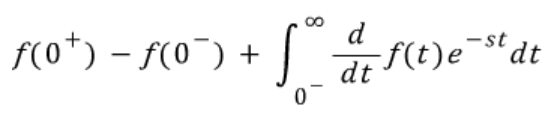
따라서 이를 본 식에 대입하여보면
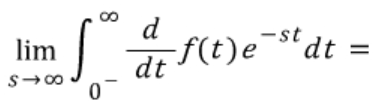
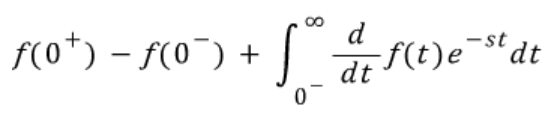
이렇게 정리가 되고 뒤에있는 두 식은 극한을 취해주면 0으로 바뀌므로 최종적으로는
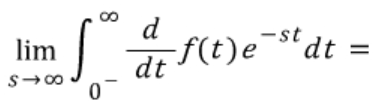
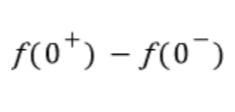
이후에 s 도메인으로의 라플라스 변환을 해주면
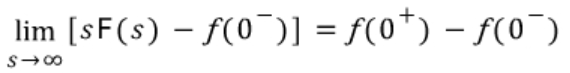
이러한 식이 남게 되고 양변에 같은 항인 f(0-)를 소거해주게 되면
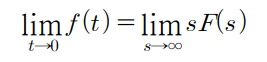
이렇게 초기값 정리가 성립되게 된다.
2. 라플라스 변환 식에서 시작
하단의 링크에 있는 곳에서 라플라스 변환식으로부터 초기값 정리를 도출해내는 과정을 잘 설명해주고 있다.
+ 디랙 델타 함수에 대한 설명도 아주 잘 나와있다.
라플라스 변환의 성질(Properties of Laplace Transform)
물리학, 수학, 전자파
ghebook.blogspot.com
최종값 정리
1차도함수의 라플라스 변환으로 부터의 최초값정리 중간에 나온 식을 가져와서
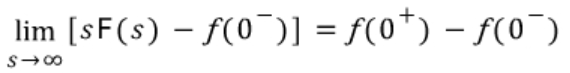
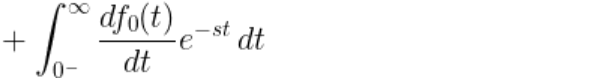
양변에 같은항을 소거해주고
이 식에서 s를 0으로 보내는 극한을 취해주어
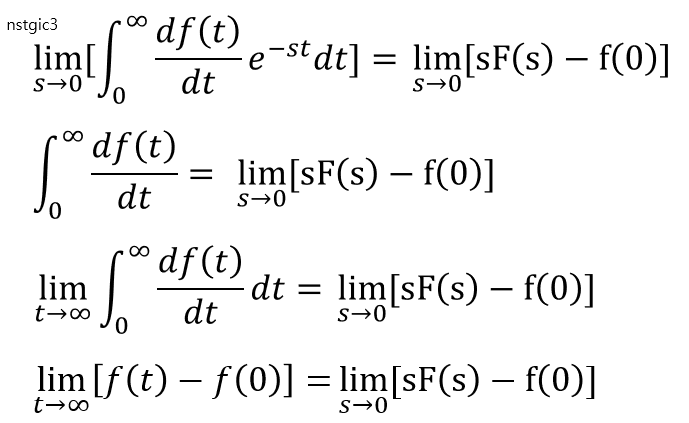
다음과 같이 식을 정리해낼수 있다.
이후에 양변에 동일한 f(0) 값은 소거해 내면 최종값 정리의 형태가 나오게 된다.
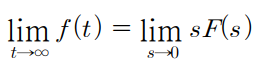
'Engineering' 카테고리의 다른 글
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
|---|---|
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
| 라플라스 폴 (0) | 2022.09.21 |
| Laplace Transformation 라플라스 변환 (0) | 2022.09.21 |
목차
개요
이전 시간에 라플라스의 개념과 성립 조건, 특성들을 배웠는데 이어서 최종값과 최초값 정리를 알아보자.
Laplace Transformation 라플라스 변환
목차 개요 Linear ordinary differential equation(선형 상미분방정식)의 해를 구하는 방식으로 많이 쓰인다. 어렵게 생각하지말고 수학자들이 만든 해를 쉽게 구하는 방식이라고 보면 된다.(수학적으로 유
nstgic3.tistory.com
둘다 라플라스 변환의 미분식에서 유도가 되며 이전 내용에 대한 충분한 이해가 있어야한다.
초기값 정리
두가지 방법으로 초기값 정리를 증명 해낼 수 있는데 (사실 순서만 좀 다를뿐이다.)
둘다 라플라스 변환 + 0에서의 불연속성을 고려한 디랙 델타 함수를 이용한 변형식에서 시작된다는 사실은 같다.
1. 1차 도함수의 라플라스 변환에서 시작
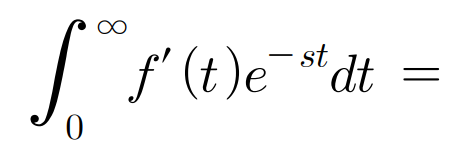
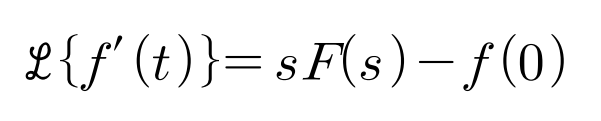
0에서 불연속한 경우에 0- 로 시작하는 함수로 고려해야지 t=0에서의 불연속점이 존재하였을때 수학적으로 성립함을 보여줄 수 있기 때문에 (단위 계단 함수의 성질)
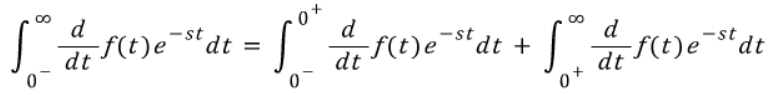
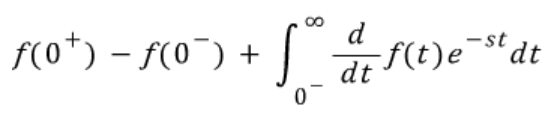
따라서 이를 본 식에 대입하여보면
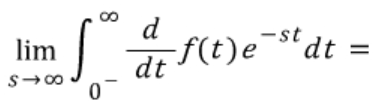
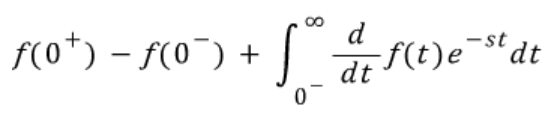
이렇게 정리가 되고 뒤에있는 두 식은 극한을 취해주면 0으로 바뀌므로 최종적으로는
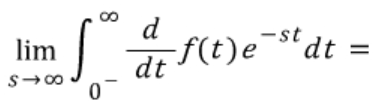
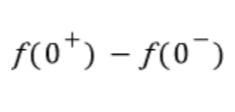
이후에 s 도메인으로의 라플라스 변환을 해주면
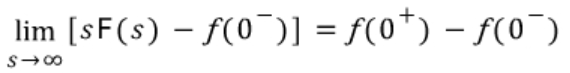
이러한 식이 남게 되고 양변에 같은 항인 f(0-)를 소거해주게 되면
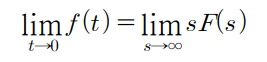
이렇게 초기값 정리가 성립되게 된다.
2. 라플라스 변환 식에서 시작
하단의 링크에 있는 곳에서 라플라스 변환식으로부터 초기값 정리를 도출해내는 과정을 잘 설명해주고 있다.
+ 디랙 델타 함수에 대한 설명도 아주 잘 나와있다.
라플라스 변환의 성질(Properties of Laplace Transform)
물리학, 수학, 전자파
ghebook.blogspot.com
최종값 정리
1차도함수의 라플라스 변환으로 부터의 최초값정리 중간에 나온 식을 가져와서
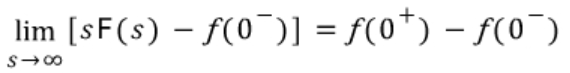
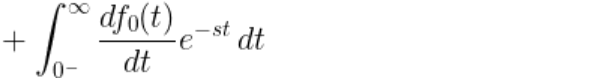
양변에 같은항을 소거해주고
이 식에서 s를 0으로 보내는 극한을 취해주어
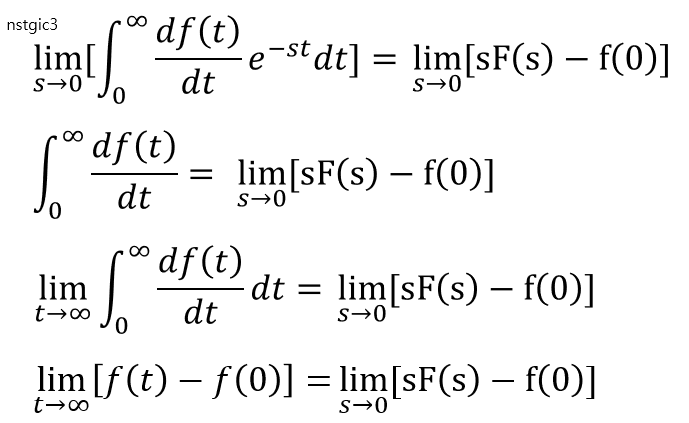
다음과 같이 식을 정리해낼수 있다.
이후에 양변에 동일한 f(0) 값은 소거해 내면 최종값 정리의 형태가 나오게 된다.
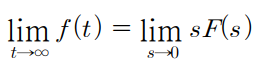
'Engineering' 카테고리의 다른 글
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
|---|---|
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
| 내리흐름 Downwash & 유도항력 Induced drag (0) | 2022.09.21 |
| 라플라스 폴 (0) | 2022.09.21 |
| Laplace Transformation 라플라스 변환 (0) | 2022.09.21 |
