목차
개요
이전 포스팅에서는 여러가지 공식들을 이용하여 만들어낸 Horseshoe vortex라는 가상의 모델을 이용해 Lifting line theory 에 대해서 알아보았다.
그럼 이렇게 만들어진 날개위의 양력분포 형상에 대해서 알게되면 무엇이 좋을까?
설계를 할 당시에 각 부분에 걸리게 되는 힘을 알게되어 시뮬레이션을 통하여 역학적 해석이 가능하다. 쉽게 말해 이러한 관계 해석을 무시하고 제작을 하여 인력을 이용하여 실험을 하는 리스크를 감수하지 않아도 된다. (결국엔 공학이 존재하는 이유를 설명)
이해를 위해 일반적인 양력 분포를 설명하기 전에 타원형 양력 분포에 대해서 먼저 설명을 하겠다.
Elliptical Lift Distribution
양력분포를 타원형으로 가정한다. 타원형으로 먼저 접근을 한 이유는 이전 포스팅에서 다뤘던 Lifting line theory 의 모든 trailing vortex 가 동등한 힘을 가질 때 나타나는 모양이 타원형과 비슷해서 이다.
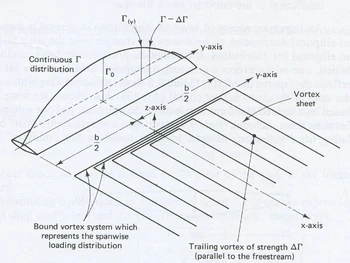
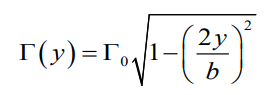
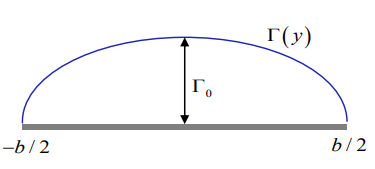
Γ0는 원점에서의 circulation 최대값, 루트 내에 들어있는 수식은 타원 기본형 공식에서 유도되었고
wing에서의 span 방향은 y이므로 y에 대한식으로 표현하였다.
여기에서 구해낸 타우를 Kutta-Joukowski 정리를 이용하면 (각 섹션의 Lift의 분포도 Elliptic 할 것이다.)
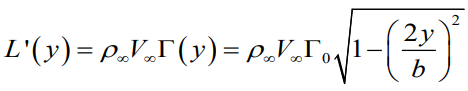
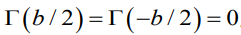
날개 끝에서의 타우는 0이라는 조건도 만족하게 된다.(위 아래 압력이 같아서)
circulation의 값이 0이 되어야한다. 루트 내의 값이 0 이 된다.
여기서 한번 더 상기해야하는것이 날개의 형상에 따른 분포를 알아본것이 아니라 분포가 타원형이라고 가정하고 그때의 분포 정도를 확인한 것이다.
그래서 이때의 공기역학적 특성은 어떨까? downwash의 분포 값을 알아보자.
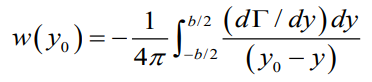
위의 일반적인 식에 타원형이라고 가정한 타우 값을 대입해주게 된다면 아래와 같이 나오게 된다.
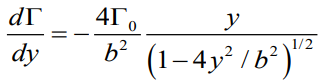
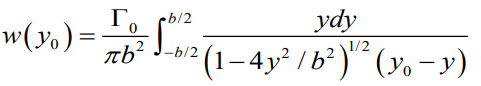
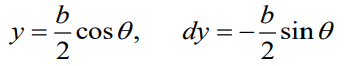
타원의 특성을 이용해서 치환 적분 + Glauert integral
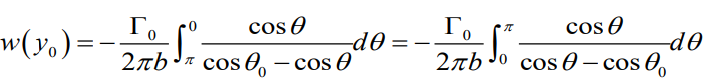
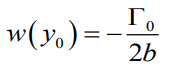
결과값을 알아보면 downwash 는 모든 span 방향의 지점에서 같은 값을 나타낸다.
항상 일정한 값을 띈다.
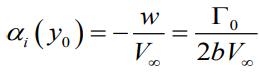
downwash 의 강도가 일정해진다. 또한 유도 받음각 또한 일정해진다.
날개의 양력분포가 타원형이면 발생하는 내리흐름이 모든 span에서 일정해진다.
타원형 양력 분포에서의 양력과 유도 받음각
1. 타원형 양력 분포에서의 양력
Total lift at Elliptical Lift distribution
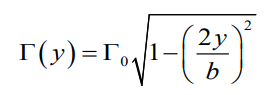
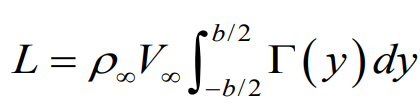
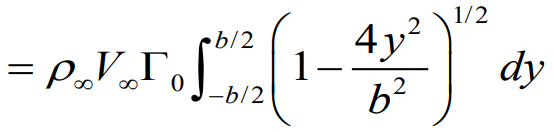
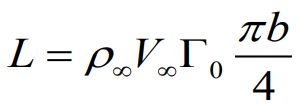
2. 타원형 양력 분포에서의 양력과 양력 공식을 이용한 circulation 표현
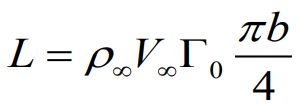
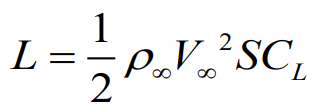
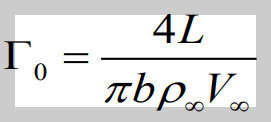
3. 2에서 구한 circulation을 타원형 양력분포에서의 유도 받음각에 적용한 표현
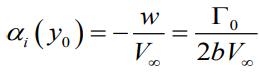
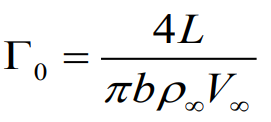
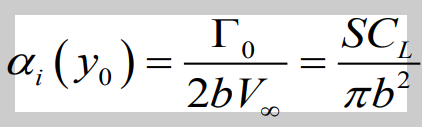
Aspect Ratio AR비, 가세비
날개의 긴방향의 길이/짧은 방향의 길이의 성분으로 항공역학에서 꽤나 의미있는 비율 이기 때문에 양항력 공식등에 적용을 해준다.
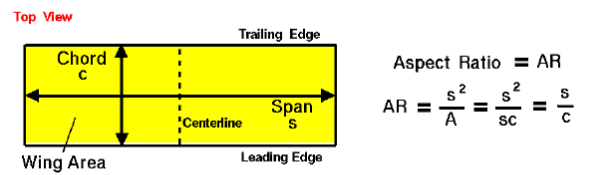
우리는 쭉 포스팅을 해오면서 긴 날개의 길이를 (b)로 두었으니 이에 맞추어서 표현해보자
그리고 위에서 최종적으로 구해낸 유도 받음각을 AR로 치환하여 표현해보면
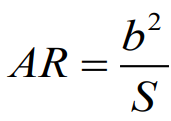

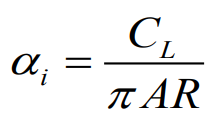
타원형 양력 분포에서의 유도 항력
일반적인 항력계수를 구하는 공식
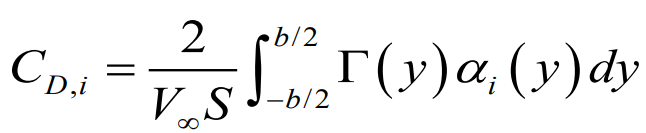
하지만 타원형 양력 분포에서는 유도 받음각이 일정하기 때문에 적분식 내에서 빠져나올수 있다.
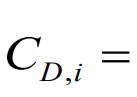
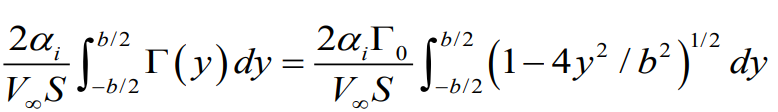
삼각 치환법을 이용하여 적분을 완료하면
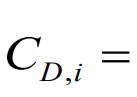
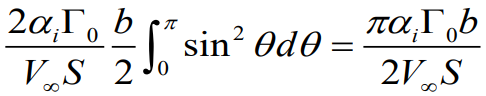
또한 유도 받음각과 circulation 도 위에 구해낸 표현식으로 치환하여 표현하자면
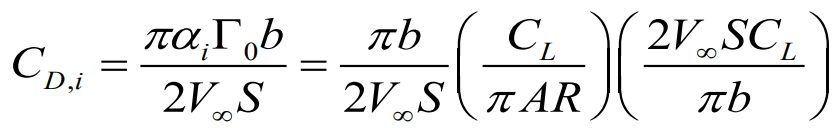
최종적으로 아래와 같은 식이 도출되게 된다.
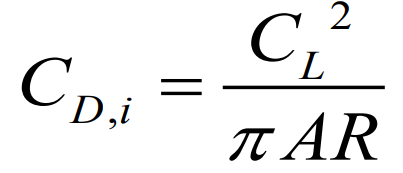
분모에 AR 성분으로 치환되어있는 모습을 볼 수있는데 AR비가 커질수록 유도항력이 작아진다는 사실을 확인 할 수있다.
글라이더의 날개가 긴 이유
유도 항력은 결국에 양력에 의해서 형성이 되는데
2022.09.21 - [Engineering] - 내리흐름 Downwash & 유도항력 Induced drag 참고
비행체에 유도 항력이 주는 영향을 알아보자면
높은 양력이 필요한 이착륙시에 유도 항력의 크기는 더욱 커지게 되고 일정 속도로 순항 할때는 전체 항력의 약 25% 정도를 차지하게 된다.
따라서 양력 형성 즉 비행기가 뜨게 하는 정도를 방해하는 힘의 4분의 1 정도가 유도항력이 차지하고 있다는 것이다.
다시 글라이더로 돌아가보자면 위에서 익힌 AR비가 길수록 날개가 좌우로 길쭉해지게 되는데 따로 추력기관이 존재하지 않는 글라이더의 경우엔 고도를 유지하는 것이 중요하다. 다시말해 양력을 유지하는 것이 중요한 것인데 이러한 양력에 반하는 힘인 항력을 줄이기 위해서는 이전 포스팅에 Parasite Drag 라고 불렀던 아무리 노력을 하고 효율적인 설계를 하여도 사라지지 않는 기생충같은 항력인 Pressure 와 Viscous 압력과 점성에 의한 항력을 제외하고 남는 항력인 유도항력을 줄이는 수밖에 없다. 때마침 위에서 구한 식을 다시 살펴보자.
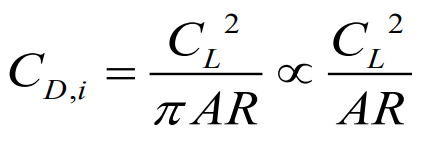
유도 항력은 결국에 양력에 의해서 형성 : 이 되는 사실도 확인이 가능하고 (C(계수) L (lift양력))
AR이 증가함에 따라서 항력 계수가 줄어드는 관계도 확인이 가능하다.
따라서 별다른 장치가 달려있지 않고 항력을 최소한으로 하는것이 유리한 글라이더에서는 AR비 즉 엄청 긴 날개를 탑재하는 것이 좋기 때문에 긴 날개를 달고 있는 것이다.

날개끝이 왜 꺾여있는지 이전 포스팅을 본 독자라면 이제 이해를 할 것이다. downwash~ winglet~
다음에는 양력분포가 타원형같은 특수 상황이 아닌 일반적인 식을 구해보고 왜 스핏파이어의 날개가 타원형인지에 대해서 알아보자
'Engineering' 카테고리의 다른 글
| AR비 그리고 Span loading (0) | 2022.10.11 |
|---|---|
| 스핏파이어의 날개 형상이 타원형인 이유 (0) | 2022.10.11 |
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
목차
개요
이전 포스팅에서는 여러가지 공식들을 이용하여 만들어낸 Horseshoe vortex라는 가상의 모델을 이용해 Lifting line theory 에 대해서 알아보았다.
그럼 이렇게 만들어진 날개위의 양력분포 형상에 대해서 알게되면 무엇이 좋을까?
설계를 할 당시에 각 부분에 걸리게 되는 힘을 알게되어 시뮬레이션을 통하여 역학적 해석이 가능하다. 쉽게 말해 이러한 관계 해석을 무시하고 제작을 하여 인력을 이용하여 실험을 하는 리스크를 감수하지 않아도 된다. (결국엔 공학이 존재하는 이유를 설명)
이해를 위해 일반적인 양력 분포를 설명하기 전에 타원형 양력 분포에 대해서 먼저 설명을 하겠다.
Elliptical Lift Distribution
양력분포를 타원형으로 가정한다. 타원형으로 먼저 접근을 한 이유는 이전 포스팅에서 다뤘던 Lifting line theory 의 모든 trailing vortex 가 동등한 힘을 가질 때 나타나는 모양이 타원형과 비슷해서 이다.

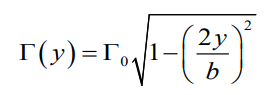

Γ0는 원점에서의 circulation 최대값, 루트 내에 들어있는 수식은 타원 기본형 공식에서 유도되었고
wing에서의 span 방향은 y이므로 y에 대한식으로 표현하였다.
여기에서 구해낸 타우를 Kutta-Joukowski 정리를 이용하면 (각 섹션의 Lift의 분포도 Elliptic 할 것이다.)
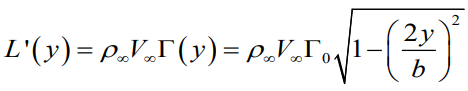
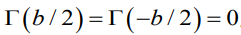
날개 끝에서의 타우는 0이라는 조건도 만족하게 된다.(위 아래 압력이 같아서)
circulation의 값이 0이 되어야한다. 루트 내의 값이 0 이 된다.
여기서 한번 더 상기해야하는것이 날개의 형상에 따른 분포를 알아본것이 아니라 분포가 타원형이라고 가정하고 그때의 분포 정도를 확인한 것이다.
그래서 이때의 공기역학적 특성은 어떨까? downwash의 분포 값을 알아보자.
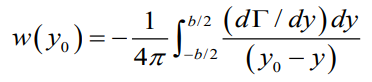
위의 일반적인 식에 타원형이라고 가정한 타우 값을 대입해주게 된다면 아래와 같이 나오게 된다.
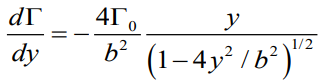
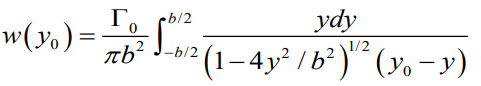
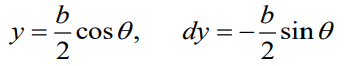
타원의 특성을 이용해서 치환 적분 + Glauert integral
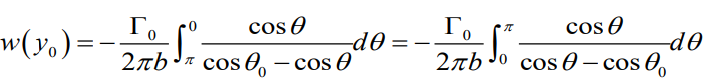
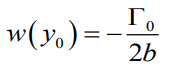
결과값을 알아보면 downwash 는 모든 span 방향의 지점에서 같은 값을 나타낸다.
항상 일정한 값을 띈다.
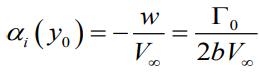
downwash 의 강도가 일정해진다. 또한 유도 받음각 또한 일정해진다.
날개의 양력분포가 타원형이면 발생하는 내리흐름이 모든 span에서 일정해진다.
타원형 양력 분포에서의 양력과 유도 받음각
1. 타원형 양력 분포에서의 양력
Total lift at Elliptical Lift distribution
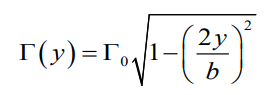
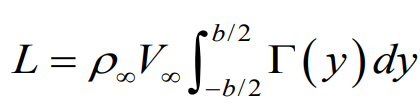
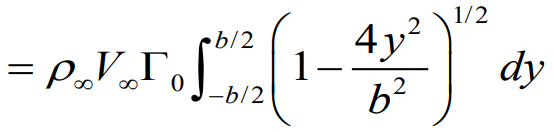
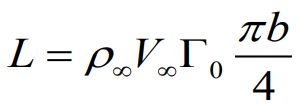
2. 타원형 양력 분포에서의 양력과 양력 공식을 이용한 circulation 표현
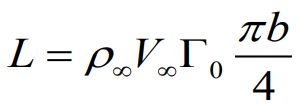
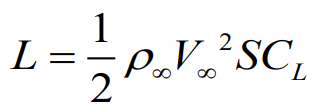
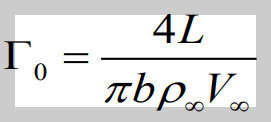
3. 2에서 구한 circulation을 타원형 양력분포에서의 유도 받음각에 적용한 표현
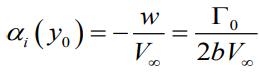
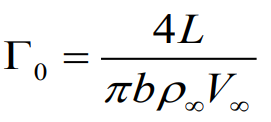
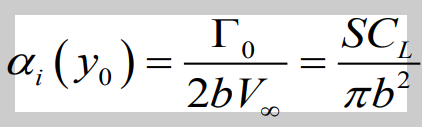
Aspect Ratio AR비, 가세비
날개의 긴방향의 길이/짧은 방향의 길이의 성분으로 항공역학에서 꽤나 의미있는 비율 이기 때문에 양항력 공식등에 적용을 해준다.

우리는 쭉 포스팅을 해오면서 긴 날개의 길이를 (b)로 두었으니 이에 맞추어서 표현해보자
그리고 위에서 최종적으로 구해낸 유도 받음각을 AR로 치환하여 표현해보면
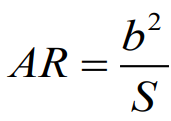

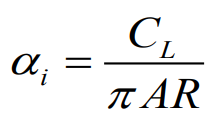
타원형 양력 분포에서의 유도 항력
일반적인 항력계수를 구하는 공식
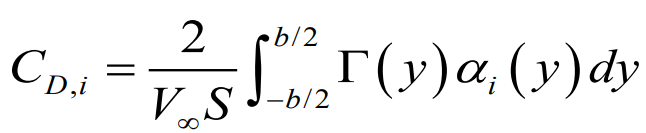
하지만 타원형 양력 분포에서는 유도 받음각이 일정하기 때문에 적분식 내에서 빠져나올수 있다.
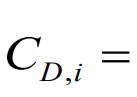
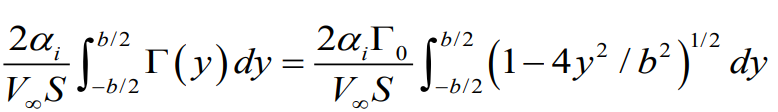
삼각 치환법을 이용하여 적분을 완료하면
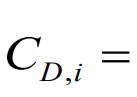
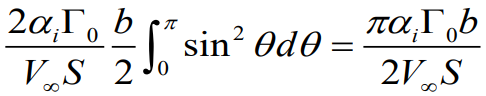
또한 유도 받음각과 circulation 도 위에 구해낸 표현식으로 치환하여 표현하자면
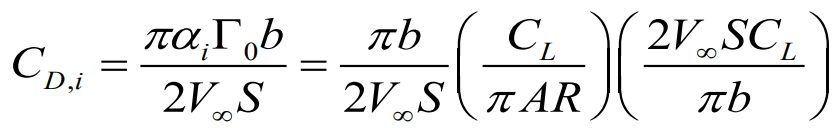
최종적으로 아래와 같은 식이 도출되게 된다.
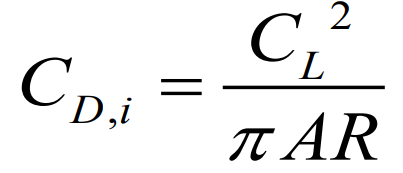
분모에 AR 성분으로 치환되어있는 모습을 볼 수있는데 AR비가 커질수록 유도항력이 작아진다는 사실을 확인 할 수있다.
글라이더의 날개가 긴 이유
유도 항력은 결국에 양력에 의해서 형성이 되는데
2022.09.21 - [Engineering] - 내리흐름 Downwash & 유도항력 Induced drag 참고
비행체에 유도 항력이 주는 영향을 알아보자면
높은 양력이 필요한 이착륙시에 유도 항력의 크기는 더욱 커지게 되고 일정 속도로 순항 할때는 전체 항력의 약 25% 정도를 차지하게 된다.
따라서 양력 형성 즉 비행기가 뜨게 하는 정도를 방해하는 힘의 4분의 1 정도가 유도항력이 차지하고 있다는 것이다.
다시 글라이더로 돌아가보자면 위에서 익힌 AR비가 길수록 날개가 좌우로 길쭉해지게 되는데 따로 추력기관이 존재하지 않는 글라이더의 경우엔 고도를 유지하는 것이 중요하다. 다시말해 양력을 유지하는 것이 중요한 것인데 이러한 양력에 반하는 힘인 항력을 줄이기 위해서는 이전 포스팅에 Parasite Drag 라고 불렀던 아무리 노력을 하고 효율적인 설계를 하여도 사라지지 않는 기생충같은 항력인 Pressure 와 Viscous 압력과 점성에 의한 항력을 제외하고 남는 항력인 유도항력을 줄이는 수밖에 없다. 때마침 위에서 구한 식을 다시 살펴보자.
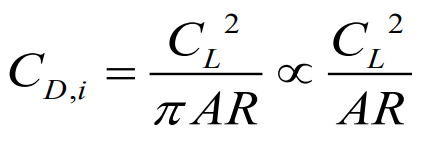
유도 항력은 결국에 양력에 의해서 형성 : 이 되는 사실도 확인이 가능하고 (C(계수) L (lift양력))
AR이 증가함에 따라서 항력 계수가 줄어드는 관계도 확인이 가능하다.
따라서 별다른 장치가 달려있지 않고 항력을 최소한으로 하는것이 유리한 글라이더에서는 AR비 즉 엄청 긴 날개를 탑재하는 것이 좋기 때문에 긴 날개를 달고 있는 것이다.

날개끝이 왜 꺾여있는지 이전 포스팅을 본 독자라면 이제 이해를 할 것이다. downwash~ winglet~
다음에는 양력분포가 타원형같은 특수 상황이 아닌 일반적인 식을 구해보고 왜 스핏파이어의 날개가 타원형인지에 대해서 알아보자
'Engineering' 카테고리의 다른 글
| AR비 그리고 Span loading (0) | 2022.10.11 |
|---|---|
| 스핏파이어의 날개 형상이 타원형인 이유 (0) | 2022.10.11 |
| Lifting-line theory 양력선 이론 자세한 설명 (2) (0) | 2022.10.06 |
| Lifting-line theory 양력선 이론 자세한 설명 (1) (0) | 2022.09.29 |
| 자유응답 1DOF 예시 Free Response (0) | 2022.09.28 |
